题目内容
【题目】设函数
，若函数
恰有两个零点，则实数
的取值范围是（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
由题意得方程
有两个不同的实数根，从而得到函数
的图象和函数
的图象有两个不同的交点，画出两函数的图象，结合图象可得所求的范围．
∵函数
恰有两个零点，
∴方程有两个不同的实数根，即方程
有两个不同的实数根，
∴函数的图象和函数的图象有两个不同的交点．
①当
时，显然不符合题意．
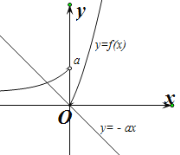
②当
时，函数的图象为过原点且斜率小于0的直线．
画出两函数的图象，如下图所示．
由图象可得两函数的图象总有两个不同的交点．
所以符合题意．
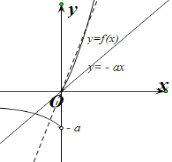
③当
时，函数的图象为过原点且斜率大于0的直线．
画出两函数的图象，如下图所示．
由图象可得，当
时，两函数的图象总有一个交点，
所以要使得两函数的图象再有一个交点，只需直线的斜率小于曲线在原点处的切线的斜率．
由
，得
，
所以
，
所以
，解得
，
所以
．
综上可得或．
故选A．
小学夺冠AB卷系列答案【题目】利用独立性检验的方法调查高中生性别与爱好某项运动是否有关，通过随机调查200名高中生是否爱好某项运动，利用
列联表，由计算可得
，参照下表：
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5,024 | 6.635 | 7.879 | 10.828 |
得到的正确结论是（ ）
A. 有99%以上的把握认为“爱好该项运动与性别无关”
B. 有99%以上的把握认为“爱好该项运动与性别有关”
C. 在犯错误的概率不超过0.5%的前提下，认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.5%的前提下，认为“爱好该项运动与性别无关”
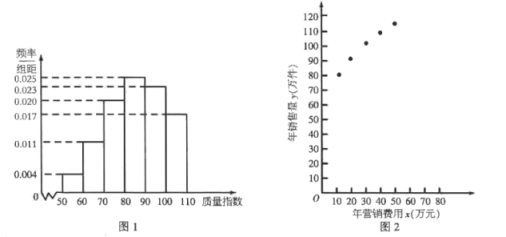
【题目】某公司生产一种产品，从流水线上随机抽取100件产品，统计其质量指数并绘制频率分布直方图（如图1）：
产品的质量指数在
的为三等品，在
的为二等品，在
的为一等品，该产品的三、二、一等品的销售利润分别为每件1.5，3.5,5.5（单位：元），以这100件产品的质量指数位于各区间的频率代替产品的质量指数位于该区间的概率.
（1）求每件产品的平均销售利润；
（2）该公司为了解年营销费用
（单位：万元）对年销售量
（单位：万件）的影响，对近5年的年营销费用
和年销售量
数据做了初步处理，得到的散点图（如图2）及一些统计量的值.
|
|
|
|
16.30 | 24.87 | 0.41 | 1.64 |
表中
，
，
，
根据散点图判断，
可以作为年销售量（万件）关于年营销费用（万元）的回归方程.
（ⅰ）建立关于的回归方程；
（ⅱ）用所求的回归方程估计该公司应投入多少营销费，才能使得该产品一年的收益达到最大？（收益=销售利润-营销费用，取
）
参考公式：对于一组数据：
，
，
，
，其回归直线
的斜率和截距的最小乘估计分别为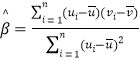
，
