题目内容
【题目】如图①，已知矩形ABCD满足AB=5，
，沿平行于AD的线段EF向上翻折（点E在线段AB上运动，点F在线段CD上运动），得到如图②所示的三棱柱
.
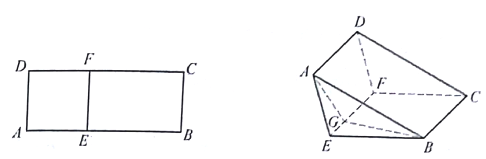
⑴若图②中△ABG是直角三角形，这里G是线段EF上的点，试求线段EG的长度x的取值范围；
⑵若⑴中EG的长度为取值范围内的最大整数，且线段AB的长度取得最小值，求二面角
的值；
⑶在⑴与⑵的条件都满足的情况下，求三棱锥A-BFG的体积.
【答案】（1）
（2）
（3）
【解析】
⑴由题设条件可知△AEG、△BEG均为直角三角形，
因此
，
.
由余弦定理
.
于是
.
.
所以，
.
又对任意
，
，
.
则
，故x的取值范围为.
⑵因为AE⊥EF，BE⊥EF，所以∠AEB就是二面角C-EF-D的平面角
又由⑴知EG的长度x为的最大整数，因此x=2.
于是
，
（
）.
因此t=2.5时，线段AB的长度取得最小值.
由此得
，
.
⑶由⑴、⑵知，
，
，
且
.
因为AE⊥EF，BE⊥EF，
.
所以EF⊥平面EAB，故
.
练习册系列答案
初中学业考试导与练系列答案
相关题目
