题目内容
设命题P：函数
在区间[-1，1]上单调递减；
命题q：函数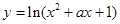
的定义域为R.若命题p或q为假命题，求
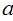的取值范围.
或
解析试题分析：利用导数求出命题
为真时
的取值集合
，利用二次函 数的知识求出命题
为真时的取值集合
，由命题p或q为假命题知，命题、均为假命题，所以的取值集合为
试题解析：解：因为
所以
函数在区间[-1，1]上单调递减
所以
即
因为当
时，
，
所以
，
因为函数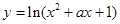的定义域为R
所以，
在
上恒成立
所以有，
，解得：
，即
由于命题p或q为假命题，所以命题、均为假命题，
所以的取值集合为＝
＝
考点：1、复合命题的真假性的判断；2，导数在研究函数性质中的应用；3、二次函数.
练习册系列答案
相关题目
＋
x＋1，其中a∈R，曲线y＝f(x)在点(1，f(1))处的切线垂直于y轴．
（e为自然对数的底数）
的单调区间；
，存在实数
，使得
成立，求实数
的取值范围
．
时，
恒成立；
时，求
的单调区间．
x3+
x2+2ax.
,+∞)上存在单调递增区间,求a的取值范围.
,求f(x)在该区间上的最大值.
x2－
的取值范围．
＋xln x，g(x)＝x3－x2－3.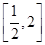
，都有f(s)≥g(t)成立，求实数a的取值范围．