题目内容
已知函数 (e为自然对数的底数)
(e为自然对数的底数)
(1)求函数 的单调区间;
的单调区间;
(2)设函数 ,存在实数
,存在实数 ,使得
,使得 成立,求实数
成立,求实数 的取值范围
的取值范围
(1) 在
在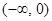 上单调递增,在
上单调递增,在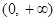 上单调递减;(2)
上单调递减;(2)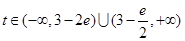
解析试题分析:(1)求导得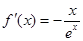 ,根据导数的符号即可求出
,根据导数的符号即可求出 的单调区间(2)如果存在
的单调区间(2)如果存在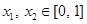 ,使得
,使得 成立,那么
成立,那么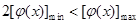 由题设得
由题设得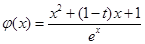 ,求导得
,求导得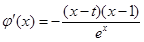 由于含有参数
由于含有参数 ,故分情况讨论,分别求出
,故分情况讨论,分别求出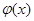 的最大值和最小值如何分类呢?由
的最大值和最小值如何分类呢?由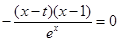 得
得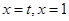 ,又由于
,又由于 故以0、1为界分类 当
故以0、1为界分类 当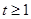 时,
时, 在
在 上单调递减;当
上单调递减;当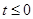 时,
时, 在
在 上单调递增以上两种情况都很容易求得
上单调递增以上两种情况都很容易求得 的范围当
的范围当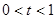 时,
时, 在
在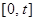 上单调递减,
上单调递减, 在
在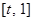 上单调递增,所以最大值为
上单调递增,所以最大值为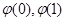 中的较大者,最小值为
中的较大者,最小值为 ,
,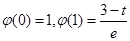 ,一般情况下再分类是比较这两者的大小,但
,一般情况下再分类是比较这两者的大小,但 ,由(1)可知
,由(1)可知 ,而
,而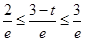 ,显然
,显然 ,所以
,所以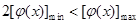 无解
无解
试题解析:(1)∵函数的定义域为R,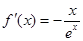 2分
2分
∴当 时,
时, ,当
,当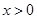 时,
时,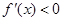
∴ 在
在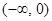 上单调递增,在
上单调递增,在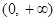 上单调递减 4分
上单调递减 4分
(2)假设存在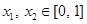 ,使得
,使得 成立,则
成立,则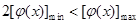 。
。
∵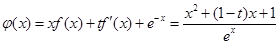
∴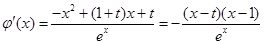 6分
6分
当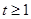 时,
时,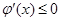 ,
, 在
在 上单调递减,∴
上单调递减,∴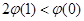 ,即
,即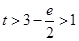
8分
②当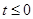 时,
时, ,
, 在
在 上单调递增,∴
上单调递增,∴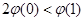 ,即
,即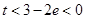
10分
③当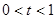 时,
时,
在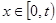 ,
, ,
, 在
在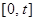 上单调递减,
上单调递减,
在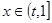 ,
, ,
, 在
在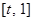 上单调递增,
上单调递增,
所以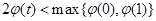 ,即
,即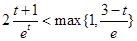

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 x2-mlnx+(m-1)x,当m≤0时,试讨论函数f(x)的单调性;
x2-mlnx+(m-1)x,当m≤0时,试讨论函数f(x)的单调性;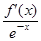 -a-2,h(x)=
-a-2,h(x)=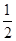 x2-2x-ln x,若x>1时总有g(x)<h(x),求实数a的取值范围.
x2-2x-ln x,若x>1时总有g(x)<h(x),求实数a的取值范围. -1.
-1. 在区间[-1,1]上单调递减;
在区间[-1,1]上单调递减;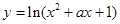 的定义域为R.若命题p或q为假命题,求
的定义域为R.若命题p或q为假命题,求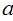 的取值范围.
的取值范围.