题目内容
已知函数f(x)=-x3+ax2+bx+c在(-∞,0)上是减函数,在(0,1)上是增函数,函数f(x)在R上有三个零点,且1是其中一个零点.
(1)求b的值 (2)求f(2)的取值范围
(1) b=0(2)
解析试题分析:(1)由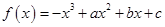 ,得:
,得: ,根据题设可判定
,根据题设可判定 ,从而解得
,从而解得 ;
;
(2)由(1)知: ,由
,由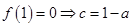 ,所以,
,所以,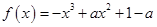
因为函数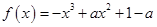 在(-∞,0)上是减函数,在(0,1)上是增函数,函数f(x)在R上有三个零点,且1是其中一个零点,所以
在(-∞,0)上是减函数,在(0,1)上是增函数,函数f(x)在R上有三个零点,且1是其中一个零点,所以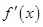 的零点
的零点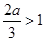 ,得到函数解析式所剩唯一参数
,得到函数解析式所剩唯一参数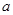 的取值范围,进而可求
的取值范围,进而可求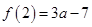 的取值范围.
的取值范围.
试题解析:
(1)∵f(x)=-x3+ax2+bx+c,
∴f ′(x)=-3x2+2ax+b. 3分
∵f(x)在(-∞,0)上是减函数,在(0,1)上是增函数,
∴当x=0时,f(x)取到极小值,即f ′(0)=0,
∴b=0. 6分
(2)由(1)知,f(x)=-x3+ax2+c,
∵1是函数f(x)的一个零点,即f(1)=0,∴c=1-a.
∵f′(x)=-3x2+2ax=0的两个根分别为x1=0,x2= . 9分
. 9分
又∵f(x)在(-∞,0)上是减函数,在(0,1)上是增函数,且函数f(x)在R上有三个零点,
∴ 应是f(x)的一个极大值点,因此应有x2=
应是f(x)的一个极大值点,因此应有x2= >1,即a>
>1,即a> .
.
∴f(2)=-8+4a+(1-a)=3a-7> .
.
故f(2)的取值范围为 . 13分
. 13分
考点:导数在研究函数性质中的应用.

练习册系列答案
相关题目
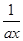 +b(a>0).
+b(a>0).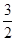 x,求a,b的值.
x,求a,b的值.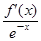 -a-2,h(x)=
-a-2,h(x)=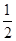 x2-2x-ln x,若x>1时总有g(x)<h(x),求实数a的取值范围.
x2-2x-ln x,若x>1时总有g(x)<h(x),求实数a的取值范围. ,其中a为正实数.
,其中a为正实数. 时,求f(x)的极值点.
时,求f(x)的极值点. ,
, ]上的单调函数,求a的取值范围.
]上的单调函数,求a的取值范围. 在区间[-1,1]上单调递减;
在区间[-1,1]上单调递减;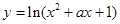 的定义域为R.若命题p或q为假命题,求
的定义域为R.若命题p或q为假命题,求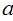 的取值范围.
的取值范围.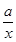 (x≠0,a∈R).
(x≠0,a∈R).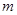 与商品单价的降低值
与商品单价的降低值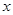 (单位:元,
(单位:元,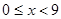 )的平方成正比,已知商品单价降低1元时,一星期多卖出5件.
)的平方成正比,已知商品单价降低1元时,一星期多卖出5件.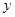 表示成
表示成 .
. 存在单调递减区间,求实数
存在单调递减区间,求实数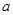 的取值范围;
的取值范围; ,求证:当
,求证:当 时,
时, 恒成立;
恒成立;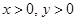 ,证明:
,证明: .
. -1.
-1.