题目内容
已知函数y=
，则该函数的值域是 ________．
[0，
]
分析：把函数y=化成整式，化成asinx+bcosx的形式，借助三角函数的有界性求解．
解答：∵y=∴3y+ycosx=1+sinx，即sinx-ycosx=3y-1
∴
=3y-1，∴sin（x+θ）=
又-1≤sin（x+θ）≤1，∴-1≤≤1
解得0≤y≤，
即函数y=的值域是[0，]．
故答案为[0，]．
点评：把asinx+bcosx化成Asin（ωx+φ）的形式，A=
，特别是a=b=1；a=
，b=1这一类特殊的角，在三角函数中常用．属中档题．
]分析：把函数y=
化成整式，化成asinx+bcosx的形式，借助三角函数的有界性求解．解答：∵y=
∴3y+ycosx=1+sinx，即sinx-ycosx=3y-1∴
=3y-1，∴sin（x+θ）=又-1≤sin（x+θ）≤1，∴-1≤
≤1解得0≤y≤
，即函数y=
的值域是[0，]．故答案为[0，
]．点评：把asinx+bcosx化成Asin（ωx+φ）的形式，A=
，特别是a=b=1；a=，b=1这一类特殊的角，在三角函数中常用．属中档题． 
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
已知函y=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的图象如图所示，则该函数的解析式中（ ）
A、ω=2，φ=
| ||
B、ω=2，φ=
| ||
C、ω=1，φ=
| ||
D、ω=1，φ=
|
已知函数y=y=
π
π
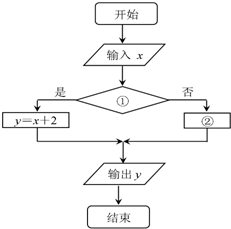
流程图表示的是给定x值，求其相应函数值的算法．请将该流程图补充完整．其中①处应填 ，②处应填 ．若输入x=3，则输出结果为 ．