题目内容
已知椭圆 的上顶点为
的上顶点为 ,直线
,直线 交椭圆于
交椭圆于 两点,设直线
两点,设直线 的斜率分别为
的斜率分别为 .
.

(1)若 时,求
时,求 的值;
的值;
(2)若 时,证明直线
时,证明直线 过定点.
过定点.
(1)  (2)详见解析
(2)详见解析
【解析】
试题分析:(1)求斜率关系,通法为从坐标出发:将直线方程代入椭圆方程得: 解出
解出 从而
从而
 因此
因此 (2)动直线过定点,关键研究出动直线方程中不变的量:由直线特殊情况分析可得m必为常数:由
(2)动直线过定点,关键研究出动直线方程中不变的量:由直线特殊情况分析可得m必为常数:由 知
知 即
即 因此利用韦达定理代入化简:
因此利用韦达定理代入化简: 所以
所以 所以直线过定点
所以直线过定点
试题解析:(1)将直线方程代入椭圆方程得: 2分
2分
解得 4分
4分
所以
 6分
6分
所以 8分
8分
(2) 设 将直线方程代入椭圆方程得:
将直线方程代入椭圆方程得: 10分
10分
则
由 知
知 12分
12分
化简得
将 代入化简得
代入化简得
所以 14分
14分
所以直线过定点 16分
16分
考点:直线与椭圆位置关系

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 ,
, __________.
__________.
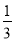 C.
C.  D.
D. 
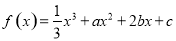 有两个极值点
有两个极值点 ,则直线
,则直线 的斜率的取值范围是
的斜率的取值范围是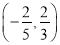 B.
B. 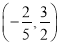 C.
C.  D.
D. 
 和圆
和圆 的位置关系为
的位置关系为 为圆
为圆 外一点,圆M上存在点T使得
外一点,圆M上存在点T使得 则实数
则实数 的取值范围是
的取值范围是  的平均数为
的平均数为 ,则该组样本数据的方差为
,则该组样本数据的方差为  的图像向左平移个
的图像向左平移个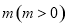 单位长度后,所得的图像关于
单位长度后,所得的图像关于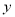 轴对称,则
轴对称,则 的最小值是
的最小值是 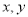 满足约束条件
满足约束条件 ,若目标函数
,若目标函数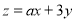 仅在点(1,0)处取得最小值,则a的取值范围为_________.
仅在点(1,0)处取得最小值,则a的取值范围为_________.