题目内容
2．求函数y=$\sqrt{-1-2cosx}$的定义域．分析 直接利用函数的定义域的求法结合余弦函数的定义域求解即可．
解答 解：要使函数y=$\sqrt{-1-2cosx}$有意义，可得-1-2cosx≥0，即，cosx≤$-\frac{1}{2}$，
解得x∈[2k$π+\frac{2π}{3}$，2k$π+\frac{4π}{3}$]，k∈Z．
函数y=$\sqrt{-1-2cosx}$的定义域：[2k$π+\frac{2π}{3}$，2k$π+\frac{4π}{3}$]，k∈Z．
点评 本题考查三角函数的定义域的求法，三角函数线的应用，考查计算能力．
练习册系列答案
相关题目
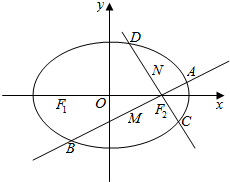已知椭圆C：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左、右焦点分别为F1，F2，且F1，F2与短轴的一个顶点Q构成一个等腰直角三角形，点P（$\frac{\sqrt{2}}{2}$，$\frac{\sqrt{3}}{2}$）在椭圆C上．