题目内容
已知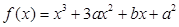 在
在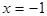 时有极值0.
时有极值0.
(Ⅰ)求常数 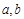 的值;
的值;
(Ⅱ)求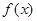 的单调区间;
的单调区间;
(Ⅲ)方程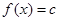 在区间[-4,0]上有三个不同的实根时实数
在区间[-4,0]上有三个不同的实根时实数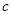 的范围.
的范围.
【答案】
(1)
(2) 的减函数区间为
的减函数区间为 ,
, 的增函数区间为
的增函数区间为 或
或
(3)
【解析】本试题主要是考查极值的概念的运用,以及运用导数求解函数的单调区间,并能进而确定方程的根的问题,通过函数的图像的极值情况,分离参数法求解参数的取值范围,转换为两个图像的交点问题来解决,这种思想尤为重要。
解:

②当 时,
时,
故方程 有根
有根 或
或 ……………………6分
……………………6分
|
x |
|
|
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
↑ |
极大值 |
↓ |
极小值 |
↑ |
由表可见,当 时,
时, 有极小值0,故
有极小值0,故 符合题意
……8分
符合题意
……8分
由上表可知: 的减函数区间为
的减函数区间为
 的增函数区间为
的增函数区间为 或
或 ………………9分
………………9分
③因为 ,
,
由数形结合可得 .
.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目







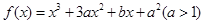 在
在 时有极值0。
时有极值0。 的值;
的值; 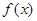 的单调区间。
的单调区间。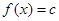 在区间[-4,0]上有三个不同的实根时实数
在区间[-4,0]上有三个不同的实根时实数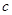 的范围。
的范围。 在
在 时有极值0.
时有极值0. 的单调区间.
的单调区间. 在
在 时有极值0.
时有极值0. 的值;
的值;  的单调区间;
的单调区间; 在区间[-4,0]上有三个不同的实根时实数
在区间[-4,0]上有三个不同的实根时实数 的范围.
的范围. 在
在 时有极值0,则
时有极值0,则 的值为 .
的值为 .