Question

（08年三校联考文）已知在时有极值0。

          （I）求常数a、b的值；

（II）求的单调区间。

Answer 1

解析：（I），由题知：

   

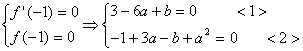
    联立<1>、<2>有：或………………4分

    当时，

    这说明此时为增函数，无极值，舍去………………6分

    当时，

    故方程有根或

x
	＋	0	－	0	＋
	↑	极大值	↓	极小值	↑

    由表可见，当时，有极小值0，故符合题意…………9分

    （II）由上表可知：的减函数区间为

    的增函数区间为或………………12分