题目内容
5.已知函数f(x)=log2$\frac{x-1}{x+1}$.(1)求函数f(x)的定义域A;
(2)设集合B={x|(x-a)(x-a-2)<0},若A∩B=B,求实数a的取值范围.
分析 (1)利用真数大于0,可得函数f(x)的定义域A;
(2)化简集合B,利用A∩B=B,B⊆A,进而a+2≤-1或a≥1,即可求实数a的取值范围.
解答 解:(1)由题意$A=\left\{{x\left|{\frac{x-1}{x+1}>0}\right.}\right\}$={x|x>1或x<-1},即A=(-∞,-1)∪(1,+∞)…(6分)
(2)B={x|(x-a)(x-a-2)<0}=(a,a+2).
因为A∩B=B,所以B⊆A,进而a+2≤-1或a≥1,
故a≤-3或a≥1…(8分)
点评 本题考查对数函数,考察集合的包含关系,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
10.现有一段长为18m的铁丝,要把它围成一个底面一边长为另一边长2倍的长方体形状的框架,当长方体体积最大时,底面的较短边长是( )
| A. | 1 m | B. | 1.5 m | C. | 0.75 m | D. | 0.5 m |
17.如图所示是水平放置的三角形的直观图,AB与y轴平行,AB=OA,则三角形AOB是( )
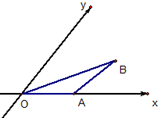

| A. | 等边三角形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |