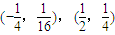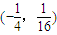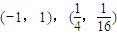题目内容
已知曲线y=x2 在点(n,n2) 处的切线方程为| x |
| an |
| y |
| bn |
(1)求an、bn 关于n 的表达式;
(2)设cn=
| 1 |
| an+bn |
| 4 |
| 3 |
(3)设dn=
| 4an |
| λ•4an+1-λ |
| nλ+λ-1 |
| λ2 |
分析:(1)对函数求导可得y′=2x,根据导数的几何意义可求切线斜率k,进而可得切线方程,即可
(2)由cn=
=
<
=2(
-
),利用裂项求和可证
(3)由dn=
可得,dn-
=
,由0<λ<1可得
<
可证
(2)由cn=
| 1 | ||
n2+
|
| 4 |
| (2n+1)•2n |
| 4 |
| (2n-1)(2n+1) |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
(3)由dn=
| 2n |
| λ•2n+1-λ |
| 1 |
| λ |
| λ-1 |
| λ(λ•2n+1-λ) |
| 1 |
| λ•2n+1-λ |
| 1 |
| λ•2n |
解答:解:(1)对函数求导可得y′=2x,根据导数的几何意义可得在点(n,n2)处的切线斜率k=2n
故所求切线方程为y-n2=2n(x-n) 即
-
=1
∴an=
,bn=n2
(2)cn=
=
<
=2(
-
)
当n=1 时,左边=
< 右边,不等式成立;…(6分)
当n≥2 时,c1+c2+…+cn<c1+2(
-
+
-
+…+
-
)
=
+2(
-
)<
∴c1+c2+…+cn<
(n∈N*)
(3)dn=
,dn-
=
∵0<λ<1,∴
<0,λ•2n+1-λ>λ•2n>0,∴
<
所以dn-
=
>
•
=
•
(d1-
)+(d2-
)+…+(dn-
)>
(
+
+…+
)
∵
<0,
+
+…+
=1-
<1,
∴
(
+
+…+
)>
,
∴(d1-
)+(d2-
)+…+(dn-
)>
∴d1+d2+…+dn>
+
=
故所求切线方程为y-n2=2n(x-n) 即
| x | ||
|
| y |
| n2 |
∴an=
| n |
| 2 |
(2)cn=
| 1 | ||
n2+
|
| 4 |
| (2n+1)•2n |
| 4 |
| (2n-1)(2n+1) |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
当n=1 时,左边=
| 2 |
| 3 |
当n≥2 时,c1+c2+…+cn<c1+2(
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2n+1 |
| 4 |
| 3 |
∴c1+c2+…+cn<
| 4 |
| 3 |
(3)dn=
| 2n |
| λ•2n+1-λ |
,dn-
| 1 |
| λ |
| λ-1 |
| λ(λ•2n+1-λ) |
∵0<λ<1,∴
| λ-1 |
| λ |
| 1 |
| λ•2n+1-λ |
| 1 |
| λ•2n |
所以dn-
| 1 |
| λ |
| λ-1 |
| λ(λ•2n+1-λ) |
| λ-1 |
| λ |
| 1 |
| λ•2n |
| λ-1 |
| λ2 |
| 1 |
| 2n |
(d1-
| 1 |
| λ |
| 1 |
| λ |
| 1 |
| λ |
| λ-1 |
| λ2 |
| 1 |
| 21 |
| 1 |
| 22 |
| 1 |
| 2n |
∵
| λ-1 |
| λ2 |
| 1 |
| 21 |
| 1 |
| 22 |
| 1 |
| 2n |
| 1 |
| 2n |
∴
| λ-1 |
| λ2 |
| 1 |
| 21 |
| 1 |
| 22 |
| 1 |
| 2n |
| λ-1 |
| λ2 |
∴(d1-
| 1 |
| λ |
| 1 |
| λ |
| 1 |
| λ |
| λ-1 |
| λ2 |
∴d1+d2+…+dn>
| n |
| λ |
| λ-1 |
| λ2 |
| nλ+λ-1 |
| λ2 |
点评:本题主要考查了利用导数的几何意义求解函数在一点的切线方程,数列求和的裂项求和及放缩法证明不等式的知识的综合应用

练习册系列答案
相关题目
已知曲线y=x2在点P处切线与直线3x-y+1=0的夹角为45°,那么点P坐标为( )
| A、(-1,1) | ||||||||
B、(-
| ||||||||
C、(-
| ||||||||
D、(-1,1),(
|
 ,其中n∈N*
,其中n∈N*  ,求证:
,求证: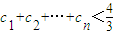 ;
;  ,其中
,其中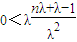 .
.