题目内容
已知曲线y=x2在点P处切线与直线3x-y+1=0的夹角为45°,那么点P坐标为( )A.(-1,1)
B.
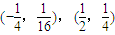
C.
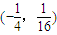
D.
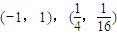
【答案】分析:可设点P处切线的斜率为k,由于切线与直线3x-y+1=0的夹角为45°,可以用两直线的夹角公式建立方程求k的值.再由导数求出切点的横坐标,进而再求纵坐标即可.
解答:解:点P处切线的斜率为k,由于切线与直线3x-y+1=0的夹角为45°,直线的斜率为3
∴ =tan45°=1
=tan45°=1
∴3-k=1+3k或3-k=-1-3k
∴k=-2,k=
又k=y′=2x,故切点的横坐标为-1或
故切点的坐标为
故选D
点评:本题考查两直线的夹角与到角问题,求解本题关键是熟练运用两直线的夹角公式求切线的斜率k,及利用导数求出切点的横坐标.夹角公式要记准,用好.
解答:解:点P处切线的斜率为k,由于切线与直线3x-y+1=0的夹角为45°,直线的斜率为3
∴
 =tan45°=1
=tan45°=1∴3-k=1+3k或3-k=-1-3k
∴k=-2,k=

又k=y′=2x,故切点的横坐标为-1或

故切点的坐标为

故选D
点评:本题考查两直线的夹角与到角问题,求解本题关键是熟练运用两直线的夹角公式求切线的斜率k,及利用导数求出切点的横坐标.夹角公式要记准,用好.

练习册系列答案
相关题目
已知曲线y=x2在点P处切线与直线3x-y+1=0的夹角为45°,那么点P坐标为( )
| A、(-1,1) | ||||||||
B、(-
| ||||||||
C、(-
| ||||||||
D、(-1,1),(
|
 ,其中n∈N*
,其中n∈N*  ,求证:
,求证: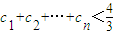 ;
;  ,其中
,其中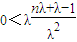 .
.