��Ŀ����
��֪ˮ���ڹ�ˮ�������Ϊ��ֵ������£���ˮʪ��ԽС��������Խ����������������ƣ���ͼ�ס�ͼ�ң�ͼ�Ĺ�ˮ����Ϊ������ABC��AB=BC����ˮʪ��l1=AB+BC ͼ�ҵĹ�ˮ����Ϊ��������ABCD��AB=CD��AD��BC����BAD=60 �㣬��ˮʪ��l2=AB+BC+CD������ABC������ABCD���������S��
��1���ֱ���l1��l2����Сֵ��
��2��Ϊʹ��������������Ʒ�����
��1���ֱ���l1��l2����Сֵ��
��2��Ϊʹ��������������Ʒ�����

�⣺��1����ͼ���У����ABC=�ȣ�AB=BC=a����S= a2sin�ȣ�
a2sin�ȣ�
��S��a��sin�Ⱦ�Ϊ��ֵ��
��a= �R
�R �����ҽ���sin��=1������=90��ʱȡ�Ⱥţ�
�����ҽ���sin��=1������=90��ʱȡ�Ⱥţ�
��l1=2a�R2 ��
��
��ͼ���У���AB=CD=m��BC=n���ɡ�BAD=60�㣬
����ã�AD=m+n��m��0��n��0����
��S= ��n+m+n��
��n+m+n�� m��
m��
���n= ��
�� ��
��
��l2=2m+n=2m+ ��
�� =
= +
+ m�R
m�R �����ҽ���
�����ҽ��� =
= m��
m��
��m= ʱȡ��=����
ʱȡ��=����
��2������ =
= ��
�� ����l2����СֵС��l1����Сֵ�����ڷ������е�l2ȡ����Сֵʱ����Ʒ���Ϊ��ѷ�����
����l2����СֵС��l1����Сֵ�����ڷ������е�l2ȡ����Сֵʱ����Ʒ���Ϊ��ѷ�����
 a2sin�ȣ�
a2sin�ȣ���S��a��sin�Ⱦ�Ϊ��ֵ��
��a=
 �R
�R �����ҽ���sin��=1������=90��ʱȡ�Ⱥţ�
�����ҽ���sin��=1������=90��ʱȡ�Ⱥţ���l1=2a�R2
 ��
����ͼ���У���AB=CD=m��BC=n���ɡ�BAD=60�㣬
����ã�AD=m+n��m��0��n��0����
��S=
 ��n+m+n��
��n+m+n�� m��
m�����n=
 ��
�� ��
����l2=2m+n=2m+
 ��
�� =
= +
+ m�R
m�R �����ҽ���
�����ҽ��� =
= m��
m����m=
 ʱȡ��=����
ʱȡ��=������2������
 =
= ��
�� ����l2����СֵС��l1����Сֵ�����ڷ������е�l2ȡ����Сֵʱ����Ʒ���Ϊ��ѷ�����
����l2����СֵС��l1����Сֵ�����ڷ������е�l2ȡ����Сֵʱ����Ʒ���Ϊ��ѷ�����
��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ

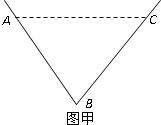 ��֪ˮ���ڹ�ˮ�������Ϊ��ֵ������£���ˮʪ��ԽС��������Խ����������������ƣ����ݶ�����ͼ��ʾ��ͼ�Ĺ�ˮ����Ϊ������ABC��AB=BC����ˮʪ��l1=AB+BC��ͼ�ҵĹ�ˮ����Ϊ��������ABCD��AD��BC��AB=CD����BAD=60�㣬��ˮʪ��l2=AB+BC+CD������ABC�͵�������ABCD���������S��
��֪ˮ���ڹ�ˮ�������Ϊ��ֵ������£���ˮʪ��ԽС��������Խ����������������ƣ����ݶ�����ͼ��ʾ��ͼ�Ĺ�ˮ����Ϊ������ABC��AB=BC����ˮʪ��l1=AB+BC��ͼ�ҵĹ�ˮ����Ϊ��������ABCD��AD��BC��AB=CD����BAD=60�㣬��ˮʪ��l2=AB+BC+CD������ABC�͵�������ABCD���������S��


 ��֪ˮ���ڹ�ˮ�������Ϊ��ֵ������£���ˮʪ��ԽС��������Խ����������������ƣ����ݶ�����ͼ��ʾ��ͼ�Ĺ�ˮ����Ϊ������ABC��AB=BC����ˮʪ��l1=AB+BC��ͼ�ҵĹ�ˮ����Ϊ��������ABCD��AD��BC��AB=CD����BAD=60�㣬��ˮʪ��l2=AB+BC+CD������ABC�͵�������ABCD���������S��
��֪ˮ���ڹ�ˮ�������Ϊ��ֵ������£���ˮʪ��ԽС��������Խ����������������ƣ����ݶ�����ͼ��ʾ��ͼ�Ĺ�ˮ����Ϊ������ABC��AB=BC����ˮʪ��l1=AB+BC��ͼ�ҵĹ�ˮ����Ϊ��������ABCD��AD��BC��AB=CD����BAD=60�㣬��ˮʪ��l2=AB+BC+CD������ABC�͵�������ABCD���������S�� ��ͼ�ڵĹ�ˮ����Ϊ��������ABCD��AB��CD��AD��BC����BAD��60�㣬��ˮʪ��
��ͼ�ڵĹ�ˮ����Ϊ��������ABCD��AB��CD��AD��BC����BAD��60�㣬��ˮʪ�� �� ����ABC������ABCD�������ΪS��
�� ����ABC������ABCD�������ΪS��
 ��
�� ����Сֵ��
����Сֵ��