题目内容
已知水渠在过水断面面积为定值的情况下,过水湿周越小,其流量越大.现有以下两种设计,如图: 图①的过水断面为等腰△ABC,AB=BC,过水湿周 .图②的过水断面为等腰梯形ABCD,AB=CD,AD∥BC,∠BAD=60°,过水湿周
.图②的过水断面为等腰梯形ABCD,AB=CD,AD∥BC,∠BAD=60°,过水湿周 . 若△ABC与梯形ABCD的面积都为S,
. 若△ABC与梯形ABCD的面积都为S,
 .图②的过水断面为等腰梯形ABCD,AB=CD,AD∥BC,∠BAD=60°,过水湿周
.图②的过水断面为等腰梯形ABCD,AB=CD,AD∥BC,∠BAD=60°,过水湿周 . 若△ABC与梯形ABCD的面积都为S,
. 若△ABC与梯形ABCD的面积都为S,
图① 图②
(1)分别求 和
和 的最小值;
的最小值;
(2)为使流量最大,给出最佳设计方案.
 和
和 的最小值;
的最小值; (2)为使流量最大,给出最佳设计方案.
解:在图①中,设∠ ,AB=BC=a.
,AB=BC=a.
则 ,
,
由于S、a、 皆为正值,可解得
皆为正值,可解得 .
.
当且仅当 ,即
,即 =90°时取等号.
=90°时取等号.
所以 ,
, 的最小值为
的最小值为 .
.
在图②中,设AB=CD=m,BC=n,由∠BAD=60°
可求得AD=m+n, ,
,
解得 .
.
 ,
,
 的最小值为
的最小值为 .
.
当且仅当 ,即
,即 时取等号.
时取等号.
(2)由于 ,则
,则 的最小值小于
的最小值小于 的最小值.所以在方案②中当
的最小值.所以在方案②中当 取得最小值时的设计为最佳方案
取得最小值时的设计为最佳方案
 ,AB=BC=a.
,AB=BC=a.则
 ,
,由于S、a、
 皆为正值,可解得
皆为正值,可解得 .
.当且仅当
 ,即
,即 =90°时取等号.
=90°时取等号.所以
 ,
, 的最小值为
的最小值为 .
.在图②中,设AB=CD=m,BC=n,由∠BAD=60°
可求得AD=m+n,
 ,
,解得
 .
.
 ,
, 的最小值为
的最小值为 .
.当且仅当
 ,即
,即 时取等号.
时取等号. (2)由于
 ,则
,则 的最小值小于
的最小值小于 的最小值.所以在方案②中当
的最小值.所以在方案②中当 取得最小值时的设计为最佳方案
取得最小值时的设计为最佳方案
练习册系列答案
相关题目

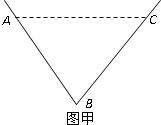 已知水渠在过水断面面积为定值的情况下,过水湿周越小,其流量越大.现有以下两种设计,其纵断面如图所示,图甲的过水断面为等腰△ABC,AB=BC,过水湿周l1=AB+BC;图乙的过水断面为等腰梯形ABCD,AD∥BC,AB=CD,∠BAD=60°,过水湿周l2=AB+BC+CD.若△ABC和等腰梯形ABCD的面积都是S,
已知水渠在过水断面面积为定值的情况下,过水湿周越小,其流量越大.现有以下两种设计,其纵断面如图所示,图甲的过水断面为等腰△ABC,AB=BC,过水湿周l1=AB+BC;图乙的过水断面为等腰梯形ABCD,AD∥BC,AB=CD,∠BAD=60°,过水湿周l2=AB+BC+CD.若△ABC和等腰梯形ABCD的面积都是S,


 已知水渠在过水断面面积为定值的情况下,过水湿周越小,其流量越大.现有以下两种设计,其纵断面如图所示,图甲的过水断面为等腰△ABC,AB=BC,过水湿周l1=AB+BC;图乙的过水断面为等腰梯形ABCD,AD∥BC,AB=CD,∠BAD=60°,过水湿周l2=AB+BC+CD.若△ABC和等腰梯形ABCD的面积都是S,
已知水渠在过水断面面积为定值的情况下,过水湿周越小,其流量越大.现有以下两种设计,其纵断面如图所示,图甲的过水断面为等腰△ABC,AB=BC,过水湿周l1=AB+BC;图乙的过水断面为等腰梯形ABCD,AD∥BC,AB=CD,∠BAD=60°,过水湿周l2=AB+BC+CD.若△ABC和等腰梯形ABCD的面积都是S,