题目内容
【题目】在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,补充在下面的问题中,并解决该问题.
这三个条件中任选一个,补充在下面的问题中,并解决该问题.
已知![]() 的内角
的内角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ______________,
______________,![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
【答案】答案不唯一,具体见解析
【解析】
(1)选①![]() ,先用余弦定理求出角
,先用余弦定理求出角![]() ,根据三角形内角和为
,根据三角形内角和为![]() 可算出角
可算出角![]() ,再由正弦定理求出
,再由正弦定理求出![]() 边,最后用三角形的面积公式
边,最后用三角形的面积公式![]() 求面积即可.
求面积即可.
(2)选②,先用正弦定理的推论将![]() 边化角,整理得角
边化角,整理得角![]() ,根据三角形内角和为
,根据三角形内角和为![]() 可算出角
可算出角![]() ,再由正弦定理求出
,再由正弦定理求出![]() 边,最后用三角形的面积公式
边,最后用三角形的面积公式![]() 求面积即可.
求面积即可.
解:(1)若选择①![]() ,
,
由余弦定理![]() ,
,
因为![]() ,所以
,所以![]() ;
;
由正弦定理![]() ,
,
得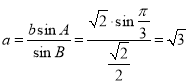 ,
,
因为![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() .
.
(2)若选择②![]() ,
,
则![]() ,
,
因为![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ;
;
由正弦定理![]() ,
,
得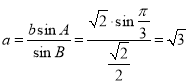 ,
,
因为![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() .
.
(3)若选择③![]() ,
,
则![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() ;
;
由正弦定理![]() ,
,
得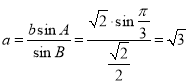 ,
,
因为![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() .
.

练习册系列答案
相关题目