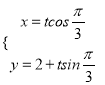题目内容
【题目】已知三棱锥![]() 中,
中, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 的中点,且
的中点,且![]() 为正三角形.
为正三角形.

(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)根据正三角形三线合一,可得![]() ,利用三角形中位线定理及空间直线夹角的定义可得
,利用三角形中位线定理及空间直线夹角的定义可得![]() ,由线面垂直的判定定理可得
,由线面垂直的判定定理可得![]() 平面
平面![]() ,即
,即![]() ,再由
,再由![]() 结合线面垂直的判定定理可得
结合线面垂直的判定定理可得![]() 平面
平面![]() ;(2)记点
;(2)记点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则有
,则有![]() ,分别求出
,分别求出![]() 的长,及
的长,及![]() 和
和![]() 面积,利用等积法可得答案.
面积,利用等积法可得答案.
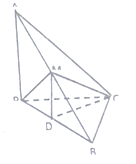
试题解析:(1)证明:如图,∵![]() 为正三角形,且
为正三角形,且![]() 为
为![]() 的中点,
的中点,
∴![]() .
.
又∵![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 的中点,
的中点,
∴![]() ,∴
,∴![]() .
.
又已知![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() .
.
又∵![]() ,
,
∴![]() 平面
平面![]() .
.
(2)解:法一:记点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则有
,则有![]()
∵![]() ∴
∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
∴![]() ,又
,又![]() ,∴
,∴![]() ,
,
在![]() 中,
中, ![]() ,又∵
,又∵![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]()
即点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
法二:∵平面![]() 平面
平面![]() 且交线为
且交线为![]() ,过
,过![]() 作
作![]() ,则
,则![]() 平面
平面![]() ,
, ![]() 的长为点
的长为点![]() 到平面
到平面![]() 的距离;
的距离;
∵![]() ,∴
,∴![]() ,又
,又![]() ,∴
,∴![]() ,∴
,∴![]() .
.
又![]() ,
,
∴![]() ,
,
∴![]() ,即点
,即点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
【方法点晴】本题主要考查的是线面垂直、棱锥的体积公式以及“等积变换”的应用,属于中档题.解题时一定要注意二面角的平面角是锐角还是钝角,否则很容易出现错误.证明线面垂直的关键是证明线线垂直,证明线线垂直常用的方法是直角三角形、等腰三角形的“三线合一”和菱形、正方形的对角线.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目