题目内容
(1)已知x<(2)已知x>0,y>0,且x+2y=1,求![]() +
+![]() 的最小值.
的最小值.
思路分析:根据题设条件,合理变形,创造能用均值定理的条件,求最值.
解:(1)∵x<![]() ,∴4x-5<0,故5-4x>0.?
,∴4x-5<0,故5-4x>0.?
∴y=4x-1+![]() =-(5-4x+
=-(5-4x+![]() )+4.?
)+4.?
∵5-4x+![]() ≥
≥![]() =2,
=2,
∴y≤-2+4=2.?
当且仅当5-4x=![]() ,即x=1或x=
,即x=1或x=![]() (舍)时,等号成立,
(舍)时,等号成立,
∴当x=1时,y取最大值为2.?
(2)∵x+2y=1,?
∴![]() +
+![]() =
=![]() +
+![]() =3+
=3+![]() +
+![]() ≥3+2
≥3+2![]() =3+2
=3+2![]() .?
.?
当且仅当![]() =
=![]() ,又x+2y=1,即x=
,又x+2y=1,即x=![]() -1,?y=1-
-1,?y=1-![]() 时等号成立.
时等号成立.
∴当x=![]() -1,y=1-
-1,y=1-![]() 时,
时, ![]() +
+![]() 取最小值3+2
取最小值3+2![]() .
.
温馨提示
用均值定理求最值时,为了满足和或积为定值的条件,常采用配,凑的方法变换,另外变量为正和等号成立的条件也要特别注意.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
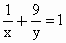 ,求x+y的最小值.
,求x+y的最小值.
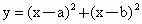 的最小值.
的最小值. (x>-2),求此函数的最小值.
(x>-2),求此函数的最小值. ,求y=4x-1+
,求y=4x-1+ 的最大值;
的最大值; 的最小值.
的最小值.