题目内容
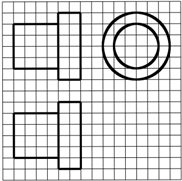如图，网格纸上正方形小格的边长为1（表示1cm），图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm，高为6c m的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由三视图判断几何体的形状，通过三视图的数据求解几何体的体积即可．
解答：
解：几何体是由两个圆柱组成，一个是底面半径为3高为2，一个是底面半径为2，高为4，
组合体体积是：32π•2+22π•4=34π．
底面半径为3cm，高为6cm的圆柱体毛坯的体积为：32π×6=54π
切削掉部分的体积与原来毛坯体积的比值为：
=
．
故答案为：
组合体体积是：32π•2+22π•4=34π．
底面半径为3cm，高为6cm的圆柱体毛坯的体积为：32π×6=54π
切削掉部分的体积与原来毛坯体积的比值为：
| 54π-34π |
| 54π |
| 10 |
| 27 |
故答案为：
| 10 |
| 27 |
点评：本题考查三视图与几何体的关系，几何体的体积的求法，考查空间想象能力以及计算能力．
练习册系列答案
相关题目
执行如图所示的程序框图，则输出的结果为（ ）
| A、4 | B、9 | C、7 | D、5 |
用一些棱长是1cm的小正方体堆放成一个几何体，其正视图和俯视图如图所示，则这个几何体的体积最多是（ ）| A、6 cm3 |
| B、7 cm3 |
| C、8 cm3 |
| D、9 cm3 |
两条不重合的直线m，n以及两个平面α，β，给出下列命题：
①若m∥α，n∥α，则m∥n；
②若m∥α，n⊥α，则m⊥n；
③若m∥n，n∥α，则m∥α；
④若m⊥α，m∥β，则α⊥β；
其中真命题的个数为（ ）
①若m∥α，n∥α，则m∥n；
②若m∥α，n⊥α，则m⊥n；
③若m∥n，n∥α，则m∥α；
④若m⊥α，m∥β，则α⊥β；
其中真命题的个数为（ ）
| A、0 | B、1 | C、2 | D、3 |
方程
-x=
+1去分母得（ ）
| 2x+3 |
| 2 |
| 9x-5 |
| 3 |
| A、3（2x+3）-x=2（9x-5）+6 |
| B、3（2x+3）-6x=2（9x-5）+1 |
| C、3（2x+3）-x=2（9x-5）+1 |
| D、3（2x+3）-6x=2（9x-5）+6 |