题目内容

若方程|x2-4x|-a=0有四个不相等的实根，则实数a的取值范围是
 
．
考点：函数的零点与方程根的关系
专题：函数的性质及应用
分析：将方程转化为函数，利用函数图象之间的关系即可得到结论．
解答： 解：由|x2-4x|-a=0得a=|x2-4x|，
作出函数y=|x2-4x|的图象，则由图象可知，要使方程|x2-4x|-a=0有四个不相等的实根，
则0＜a＜4，
故答案为：（0，4）
点评：本题主要考查函数与方程的应用，利用方程和函数之间的关系进行转化，利用数形结合是解决本题的关键．
练习册系列答案
相关题目
下列说法中：
①集合A={x|mx2-4x+4=0}中只有一个元素，则m=1；
②若f（x）=ax2+（2a+b）x+2（其中x∈[2a-1，a+4]）是偶函数，则实数b=2；
③已知函数f（x）单调递减，则f(
1-x2
)的单调递增区间为[0，1]；
④已知f（x）是定义在R上的不恒为零的函数，且对任意的x，y∈R都满足f（x•y）=x•f（y）+y•f（x），则f（x）是奇函数．
其中正确说法的序号是
 
．
讨论下列椭圆的范围，并画出图形：
（1）4x2+y2=16；
（2）5x2+9y2=100．
某机构下设A、B、C三个工作组，其分别有组员32、32、16人，现向社会公开征求意见，为搜集所征求的意见，拟采用分层抽样的方法从A、B、C三个工作小组抽取5名工作人员来完成．
（1）求从三个工作组分别抽取的人数；
（2）搜集意见结束后，若从抽取的5名工作人员中再随机抽取2名进行汇总整理，求这两名工作人员没有A组工作人员的概率；
（3）用随机抽样的方法从B工作组中抽取8人进行测试，测试成绩如下：9.4，8.6，9.2，9.6，8.7，9.3，9.0，8.2．把这8人的测试成绩看作一个总体，从中任取一个数，求该数与样本平均数之差的绝对值不超过0.5的概率．
执行如图的框图：若输出的S值满足
1
32
＜|S-1|＜
1
8
，则自然数p的值为
 
．
二次函数y=ax2+bx+c（x∈R）的部分对应值如表：
-4-3-2-10123
1040-2-20410
则不等式cx2+bx+a≥0的解集为
 
．
函数f（x）=-sin（2x+
π
4
）图象为C，以下四个结论中正确的是（写出所有正确编号）（　　）
①图象C关于直线x=
5π
8
对称；
②图象关于点（-
5π
8
，0）对称；
③函数f（x）在区间  （-
7π
8
，
3π
8
） 内是增函数； 
④由y=-sin2x的图象向左平移
π
4
个单位长度可以得到图象C．
A、①②B、①③
C、①②④D、①②③
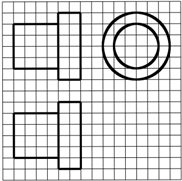如图，网格纸上正方形小格的边长为1（表示1cm），图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm，高为6c m的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为
 
．
已知x，y满足
x≥1
y≥0
x+2y-3≥0
x+2y-5≤0
，则
y
x
的最大值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网