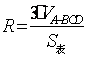题目内容
如图,ABCD是正方形,O是正方形的中心,PO 底面ABCD,E是PC的中点。
底面ABCD,E是PC的中点。
求证:(1)PA∥平面BDE (4分)
(2)平面PAC 平面BDE(6分)
平面BDE(6分)
(1)见解析(2)见解析.
解析试题分析:(1) O, E分别是是AC和 PC的中点 OE∥AP,又OE
OE∥AP,又OE 平面BDE,PA
平面BDE,PA 平面BDE,显然PA∥平面BDE得证;
平面BDE,显然PA∥平面BDE得证;
(2)由于PO 底ABCD,
底ABCD,
 PO
PO BD,又AC
BD,又AC BD
BD BD
BD 平面PAC, BD
平面PAC, BD 平面BDE
平面BDE 平面PAC
平面PAC 平面BDE
平面BDE
试题解析:证明:(1)∵O是AC的中点,E是PC的中点,
∴OE∥AP,
又∵OE 平面BDE,PA
平面BDE,PA 平面BDE,
平面BDE,
∴PA∥平面BDE
(2)∵PO 底ABCD,
底ABCD,
∴PO BD,
BD,
又∵AC BD,且AC
BD,且AC PO=O
PO=O
∴BD 平面PAC,而BD
平面PAC,而BD 平面BDE,
平面BDE,
∴平面PAC 平面BDE
平面BDE
考点:线面平行,面面垂直.

练习册系列答案
相关题目

 中,
中, ,
, ,
,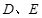 分别为
分别为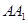 和
和 的中点.
的中点.

 平面
平面 ;(5分)
;(5分) 的体积.(7分)
的体积.(7分) 中,底面
中,底面 为直角梯形,且
为直角梯形,且 ,
, ,侧面
,侧面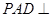 底面
底面 .
. 平面
平面 ;
; 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在,指出点
?若存在,指出点 的余弦值.
的余弦值.
 中,
中, ⊥底面
⊥底面 ,底面
,底面 ,
, ,
, 分别是
分别是 ,
, 的 中点.
的 中点. 平面
平面 ;
; ;
; 是线段
是线段 上一动点,试确定
上一动点,试确定 平面
平面 ,并证明你的结论.
,并证明你的结论.
 ,AA′=1,点M,N分别为A′B和B′C′的中点.
,AA′=1,点M,N分别为A′B和B′C′的中点.
 Sh,其中S为底面面积,h为高)
Sh,其中S为底面面积,h为高) ,⊙O为其内切圆,D为BC的中点,将三角形ACD沿AD折叠,使二面角B-AD-C成直二面角,则⊙O上的圆弧扫过的曲面面积为____________.
,⊙O为其内切圆,D为BC的中点,将三角形ACD沿AD折叠,使二面角B-AD-C成直二面角,则⊙O上的圆弧扫过的曲面面积为____________. ,则AC与平面α所成角的大小是
,则AC与平面α所成角的大小是