题目内容
18．不等式1＜|x+1|＜3的解集为（-4，-2）∪（0，2）．分析 去掉绝对值号得到关于x的不等式组，解出即可．
解答 解：∵1＜|x+1|＜3，
∴$\left\{\begin{array}{l}{-3＜x+1＜3}\\{x+1＞1或x+1＜-1}\end{array}\right.$，
解得：-4＜x＜-2或0＜x＜2，
故答案为：（-4，-2）∪（0，2）．
点评 本题考查了解绝对值不等式问题，考查分类讨论思想，是一道基础题．
练习册系列答案
相关题目
12．为了了解培训讲座对某工厂工人生产时间（生产一个零件所用的时间，单位：分钟）的影响．从工厂随机选取了200名工人，再将这200名工人随机的分成A，B两组，每组100人．A组参加培训讲座，B组不参加．培训讲座结束后A，B两组中各工人的生产时间的调查结果分别为表1和表2．
表1：
表2
（1）甲、乙两名工人是随机抽取到的200名工人中的两人，求甲、乙分在不同组的概率；
（2）完成图3的频率分布直方图，比较两组的生产时间的中位数的大小和两组工人中个体间的差异程度的大小；（不用计算，可通过直方图直接回答结论）
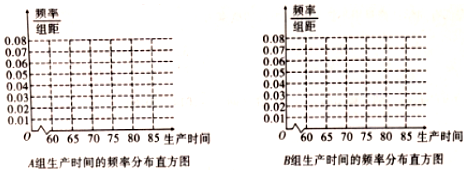
（3）完成下面2×2列联表，并回答能否有99.9%的把握认为“工人的生产时间”与参加培训讲座有关？
下面临界值表仅供参考：
${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$．
表1：
| 生产时间 | [60，65） | [65，70） | [70，75） | [75，80） |
| 人数 | 30 | 40 | 20 | 10 |
| 生产时间 | [60，65） | [65，70） | [70，75） | [75，80） | [80，85） |
| 人数 | 10 | 25 | 20 | 30 | 15 |
（2）完成图3的频率分布直方图，比较两组的生产时间的中位数的大小和两组工人中个体间的差异程度的大小；（不用计算，可通过直方图直接回答结论）
（3）完成下面2×2列联表，并回答能否有99.9%的把握认为“工人的生产时间”与参加培训讲座有关？
| 生产时间小于70分钟 | 生产时间不小于70分钟 | 合计 | |
| A组工人 | a= | b= | |
| B组工人 | c= | d= | |
| 合计 | n= |
| P（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
13．若f（x）=x3-ax2+1在（1，3）内单调递减，则实数a的范围是（ ）
| A． | [$\frac{9}{2}$，+∞） | B． | （-∞，3] | C． | （3，$\frac{9}{2}$） | D． | （0，3） |
3．函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+ax-b（x＞0）}\\{0（x=0）}\\{g（x）（x＜0）}\end{array}\right.$在区间（a+$\frac{4}{a}$，-b2+4b）上满足f（-x）+f（x）=0，则g（-$\sqrt{2}$）的值为（ ）
| A． | -2$\sqrt{2}$ | B． | 2$\sqrt{2}$ | C． | -$\sqrt{2}$ | D． | $\sqrt{2}$ |
10．函数f（x）=x2-（2a-1）x-3在$（{\frac{3}{2}，+∞}）$上是增函数，则实数a的范围是（ ）
| A． | a≤1 | B． | a≥1 | C． | a≤2 | D． | a≥2 |
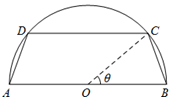一个圆柱形圆木的底面半径为1m，长为10m，将此圆木沿轴所在的平面剖成两个部分，现要把其中一个部分加工成直四棱柱木梁，长度保持不变，底面为等腰梯形ABCD（如图所示，其中O为圆心，C，D在半圆上），设∠BOC=θ，直四棱柱木梁的体积为V（单位：m3），侧面积为S（单位：m2）．