题目内容
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
(1)数列 各项均不为0,前n项和为
各项均不为0,前n项和为 ,
, ,
, 的前n项和为
的前n项和为 ,且
,且 ,若数列
,若数列 共3项,求所有满足要求的数列;
共3项,求所有满足要求的数列;
(2)求证: 是满足已知条件的一个数列;
是满足已知条件的一个数列;
(3)请构造出一个满足已知条件的无穷数列 ,并使得
,并使得 ;若还能构造其他符合要求的数列,请一并写出(不超过四个)。
;若还能构造其他符合要求的数列,请一并写出(不超过四个)。
(1) ;
; ;
; ;(2)证明见解析;(3)详见解析.
;(2)证明见解析;(3)详见解析.
【解析】
试题分析:(1)根据 求
求 ;(2)利用数学归纳法进行证明;(3)根据
;(2)利用数学归纳法进行证明;(3)根据 ,进行构造.
,进行构造.
试题解析:(1) 时,
时, 1分
1分
 时,
时,
 2分
2分
 时,
时,
当 时,
时,

当 时,
时, 3分
3分
所以符合要求的数列有: ;
; ;
; 4分
4分
(2) ,即证
,即证 ,
,
用数学归纳法证:
1. 时,
时, 成立 6分
成立 6分
2.假设 ,
, 成立 7分
成立 7分
则 时,
时,


等式也成立 9分
综合12,对于 ,都有
,都有

 是满足已知条件的一个数列。 10分
是满足已知条件的一个数列。 10分
(3) ①
①
 ②
②
②-①得
 ,
, ③ 11分
③ 11分
 时
时 ④
④
③-④得 12分
12分

 或
或
 14分
14分
构造:
ⅰ) 15分
15分
ⅱ) 16分
16分
ⅲ) 17分
17分
ⅳ) 18分.
18分.
考点:1.  的应用;2.数学归纳法;3.新定义题目.
的应用;2.数学归纳法;3.新定义题目.

 ,体积为
,体积为 ,则它的侧面积为
,则它的侧面积为  .
. ,且满足
,且满足 ,则
,则 值( )
值( )  B.-
B.- D.
D.
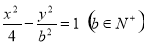 的两个焦点为
的两个焦点为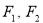 ,
, 为坐标原点,点
为坐标原点,点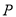 在双曲线上,且
在双曲线上,且 ,若
,若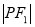 、
、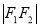 、
、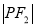 成等比数列,则
成等比数列,则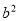 等于( )
等于( ) 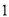 B.
B.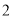 C.
C. D.
D.
 ( )
( )  上,且与x轴和抛物线的准线都相切的一个圆的方程是( )
上,且与x轴和抛物线的准线都相切的一个圆的方程是( )




 ,则方程
,则方程 只有一个根
只有一个根  且
且 ,则
,则
 ,则
,则 不成立
不成立  ,且
,且 ,那么
,那么 一定是纯虚数
一定是纯虚数 为
为 的斜边
的斜边 的延长线上一点,且
的延长线上一点,且 与
与 的外接圆相切,过点
的外接圆相切,过点 作
作 的垂线,垂足为
的垂线,垂足为 ,若
,若 ,
, ,求线段
,求线段 的长.
的长.