题目内容
如图，AP⊙O切于点A，交弦DB的延长线于点P，过点B作圆O的切线交AP于点C．若∠ACB=90°，BC=3，CP=4，则弦DB的长为______．
∵BC⊥AP，∴BP2=BC2+CP2=32+42=25，∴BP=5．
又AC与BC都是⊙O的切线，∴AC=BC=3，
由切割线定理可得PA2=PB?PD，∴72=5×（5+DB），解得DB=
．
∴弦DB的长为
．
故答案为
．
又AC与BC都是⊙O的切线，∴AC=BC=3，
由切割线定理可得PA2=PB?PD，∴72=5×（5+DB），解得DB=
| 24 |
| 5 |
∴弦DB的长为
| 24 |
| 5 |
故答案为
| 24 |
| 5 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
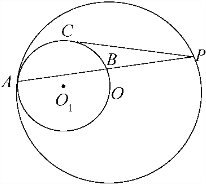如图，已知⊙O和⊙O1内切于点A，⊙O的弦AP交⊙O1于点B，PC切⊙O1于点C，且
（2013•海淀区一模）如图，AP⊙O切于点A，交弦DB的延长线于点P，过点B作圆O的切线交AP于点C．若∠ACB=90°，BC=3，CP=4，则弦DB的长为
如图，AP⊙O切于点A，交弦DB的延长线于点P，过点B作圆O的切线交AP于点C．若∠ACB=90°，BC=3，CP=4，则弦DB的长为________．