题目内容
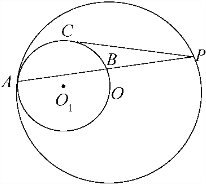 如图,已知⊙O和⊙O1内切于点A,⊙O的弦AP交⊙O1于点B,PC切⊙O1于点C,且
如图,已知⊙O和⊙O1内切于点A,⊙O的弦AP交⊙O1于点B,PC切⊙O1于点C,且| PC |
| PA |
| ||
| 2 |
分析:根据同圆的半径相等,得到两个顶角相等的等腰三角形,得到两条线段平行,根据平行线分线段成比例定理,得到比例式,又根据切割线定理得到关系式,把整理出的关系式两边同时除以PA2,得到要求的结果.
解答: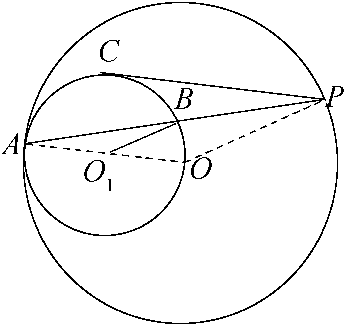 解:连接OP、OA、O1B,△OPA和△O1BA是顶角相等的等腰三角形,
解:连接OP、OA、O1B,△OPA和△O1BA是顶角相等的等腰三角形,
故∠APO=∠ABO1,从而O1B∥OP
故
=
.
又由切割线定理,知PC2=PB•PA=(PA-AB)•PA=PA2-PA•AB,两端同除以PA2,
得
=1-
,
即(
)2=1-
,
故
=
,
从而⊙O1和⊙O的半径的比值为
=
=
.
答:⊙O1和⊙O的半径的比值为
 解:连接OP、OA、O1B,△OPA和△O1BA是顶角相等的等腰三角形,
解:连接OP、OA、O1B,△OPA和△O1BA是顶角相等的等腰三角形,故∠APO=∠ABO1,从而O1B∥OP
故
| AO1 |
| AO |
| AB |
| AP |
又由切割线定理,知PC2=PB•PA=(PA-AB)•PA=PA2-PA•AB,两端同除以PA2,
得
| PC2 |
| PA2 |
| AB |
| PA |
即(
| ||
| 2 |
| AB |
| PA |
故
| AB |
| PA |
| 1 |
| 2 |
从而⊙O1和⊙O的半径的比值为
| AO1 |
| AO |
| AB |
| AP |
| 1 |
| 2 |
答:⊙O1和⊙O的半径的比值为
| 1 |
| 2 |
点评:本题考查平行线分线段成比例定理,解题的关键是两个比例式之间的变化,还有两边同时除以PA2的做法,本题是一个技巧性比较强的问题.

练习册系列答案
相关题目
 如图,已知⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为BD中点,连接AG分别交⊙O、BD于点E、F连接CE.
如图,已知⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为BD中点,连接AG分别交⊙O、BD于点E、F连接CE. (2013•长春一模)请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.
(2013•长春一模)请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.
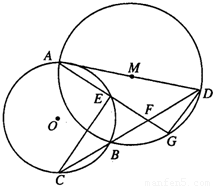 如图,已知⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为BD中点,连接AG分别交⊙O、BD于点E、F连接CE.
如图,已知⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为BD中点,连接AG分别交⊙O、BD于点E、F连接CE.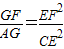 .
.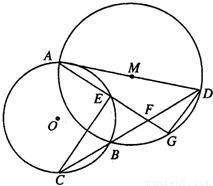 如图,已知⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为BD中点,连接AG分别交⊙O、BD于点E、F连接CE.
如图,已知⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为BD中点,连接AG分别交⊙O、BD于点E、F连接CE.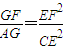 .
.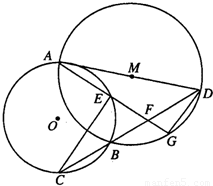 如图,已知⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为BD中点,连接AG分别交⊙O、BD于点E、F连接CE.
如图,已知⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为BD中点,连接AG分别交⊙O、BD于点E、F连接CE.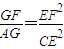 .
.