题目内容
如图,AP⊙O切于点A,交弦DB的延长线于点P,过点B作圆O的切线交AP于点C.若∠ACB=90°,BC=3,CP=4,则弦DB的长为 .
【答案】分析:在Rt△BCP中,由勾股定理可得BP,由切线长定理可得AC=BC,再利用切割线定理可得DB.
解答:解:∵BC⊥AP,∴BP2=BC2+CP2=32+42=25,∴BP=5.
又AC与BC都是⊙O的切线,∴AC=BC=3,
由切割线定理可得PA2=PB•PD,∴72=5×(5+DB),解得 .
.
∴弦DB的长为 .
.
故答案为 .
.
点评:熟练掌握勾股定理、切线长定理、切割线定理是解题的关键.
解答:解:∵BC⊥AP,∴BP2=BC2+CP2=32+42=25,∴BP=5.
又AC与BC都是⊙O的切线,∴AC=BC=3,
由切割线定理可得PA2=PB•PD,∴72=5×(5+DB),解得
 .
.∴弦DB的长为
 .
.故答案为
 .
.点评:熟练掌握勾股定理、切线长定理、切割线定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
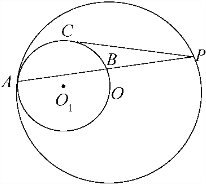 如图,已知⊙O和⊙O1内切于点A,⊙O的弦AP交⊙O1于点B,PC切⊙O1于点C,且
如图,已知⊙O和⊙O1内切于点A,⊙O的弦AP交⊙O1于点B,PC切⊙O1于点C,且 (2013•海淀区一模)如图,AP⊙O切于点A,交弦DB的延长线于点P,过点B作圆O的切线交AP于点C.若∠ACB=90°,BC=3,CP=4,则弦DB的长为
(2013•海淀区一模)如图,AP⊙O切于点A,交弦DB的延长线于点P,过点B作圆O的切线交AP于点C.若∠ACB=90°,BC=3,CP=4,则弦DB的长为 如图,AP⊙O切于点A,交弦DB的延长线于点P,过点B作圆O的切线交AP于点C.若∠ACB=90°,BC=3,CP=4,则弦DB的长为________.
如图,AP⊙O切于点A,交弦DB的延长线于点P,过点B作圆O的切线交AP于点C.若∠ACB=90°,BC=3,CP=4,则弦DB的长为________.