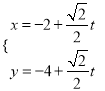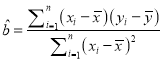Question

【题目】已知椭圆的左、右焦点分别为F1(－c，0)，F2(c，0)，直线交椭圆E于A，B两点，△ABF1的周长为16，△AF1F2的周长为12．

(1)求椭圆E的标准方程与离心率；

(2)若直线l与椭圆E交于C，D两点，且P(2，2)是线段CD的中点，求直线l的一般方程．

Answer 1

【答案】（1） （2）

【解析】试题分析：

(1)由题意可得关于的方程组，求解方程组计算可得：标准方程为，离心率为；

(2)很明显直线的斜率存在，设出点的坐标，利用点差法可得CD中点坐标为，且，利用点斜式方程可得直线l的一般方程是 .

试题解析：

（1）由题知，解得，

椭圆E的标准方程为，离心率.

（2）由（1）知，易知直线的斜率存在，设为，

设,则，，

，

又是线段CD的中点，，

故直线的方程为，化为一般形式即.