题目内容
若关于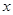 的不等式
的不等式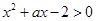 在区间
在区间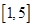 上有解,则实数
上有解,则实数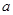 的取值范围为 ( )
的取值范围为 ( )
A.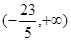 | B.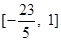 | C.(1,+∞) | D.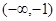 |
A
解析试题分析:问题等价转化为不等式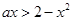 在区间
在区间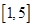 上有解,即不等式
上有解,即不等式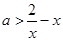 在区间
在区间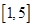 上有解,令
上有解,令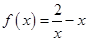 ,则有
,则有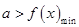 ,而函数
,而函数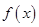 在区间
在区间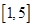 上单调递减,故函数
上单调递减,故函数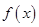 在
在 处取得最小值,即
处取得最小值,即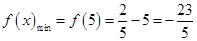 ,
,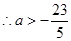 .
.
考点:一元二次不等式、参数分离法

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
不等式 的解集为( )
的解集为( )
A.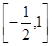 | B. | C.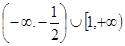 | D.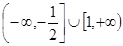 |
已知 关于
关于 的一元二次不等式
的一元二次不等式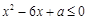 的解集中有且仅有3个整数,则所有符合条件的
的解集中有且仅有3个整数,则所有符合条件的 的值之和是( )
的值之和是( )
| A.13 | B.18 | C.21 | D.26 |
不等式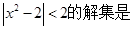
A.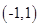 | B.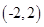 | C.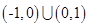 | D. |
若集合 ,则实数a的取值范围是
,则实数a的取值范围是
A.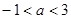 | B.1<a<4 | C.0<a<3 | D.0<a<4 |
不等式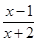 <0的解集为( )
<0的解集为( )
| A.(1,+∞) | B.(-∞,-2) |
| C.(-2,1) | D.(-∞,-2)∪(1,+∞) |
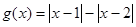 ,则
,则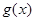 的值域为 ;若关于
的值域为 ;若关于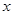 的不等式
的不等式 的解集为空集,则实数
的解集为空集,则实数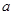 的取值范围是 .
的取值范围是 .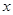 的不等式
的不等式 的解集叫
的解集叫 的
的 邻域.已知
邻域.已知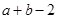 的
的 邻域为区间
邻域为区间 ,其中
,其中 、
、 分别为椭圆
分别为椭圆 的长半轴和短半轴.若此椭圆的一焦点与抛物线
的长半轴和短半轴.若此椭圆的一焦点与抛物线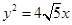 的焦点重合,则椭圆的方程为( )
的焦点重合,则椭圆的方程为( )
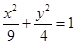

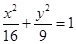
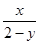 ,若关于x的不等式(x-a)⊙(x+1-a)>0的解集是集合{x|-2≤x≤2,x∈R}的子集,则实数a的取值范围是( )
,若关于x的不等式(x-a)⊙(x+1-a)>0的解集是集合{x|-2≤x≤2,x∈R}的子集,则实数a的取值范围是( )