题目内容
已知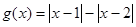 ,则
,则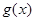 的值域为 ;若关于
的值域为 ;若关于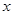 的不等式
的不等式 的解集为空集,则实数
的解集为空集,则实数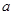 的取值范围是 .
的取值范围是 .
 (3分),
(3分),
解析试题分析:
当 时,
时, 当
当 时,
时, ,所以
,所以 当
当 时,
时, ,综上,
,综上, (此结果也可以由绝对值的几何意义直接得出),
(此结果也可以由绝对值的几何意义直接得出), 的解集为空集,就是
的解集为空集,就是 ,所以
,所以 .
.
考点:1.绝对值的意义;2. 含参绝对值不等式的解法.

练习册系列答案
相关题目
一元二次不等式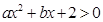 的解集是
的解集是 ,则
,则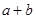 的值是( )。
的值是( )。
A.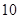 | B.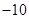 | C.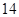 | D.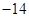 |
不等式 的解集是( )
的解集是( )
A.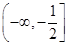 | B.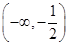 | C. | D. |
已知集合 ,则
,则 ( )
( )
A. | B.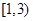 | C. | D. |
若函数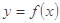 的导函数为
的导函数为 ,且
,且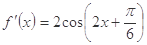 ,则
,则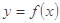 在
在 上的单调增区间为( )
上的单调增区间为( )
A. | B. |
C. 和 和 | D. 和 和 |
若关于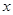 的不等式
的不等式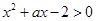 在区间
在区间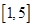 上有解,则实数
上有解,则实数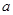 的取值范围为 ( )
的取值范围为 ( )
A.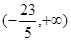 | B.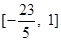 | C.(1,+∞) | D.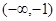 |
若不等式 与不等式
与不等式 的解集相同,则
的解集相同,则 ( )
( )
A. | B. | C. | D. |
函数 的最小值为( )
的最小值为( )
A. | B.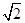 | C.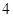 | D. |
 的解集为
的解集为  的两条直角边
的两条直角边 的长分别为3cm,4cm,以
的长分别为3cm,4cm,以 为直径的圆与
为直径的圆与 交于点
交于点 ,则
,则 .
.
 的参数方程为
的参数方程为 (
( 为参数)以原点为极点,
为参数)以原点为极点, 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为 ,则直线
,则直线