题目内容
求下列函数的单调区间:(1)y=![]() sin(
sin(![]() -
-![]() );
);
(2)y=-|sin(x+![]() )|.
)|.
剖析:(1)要将原函数化为y=-![]() sin(
sin(![]() x-
x-![]() )再求之.(2)可画出y=-|sin(x+
)再求之.(2)可画出y=-|sin(x+![]() )|的图象.
)|的图象.
解:(1)y=![]() sin(
sin(![]() -
-![]() )=-
)=-![]() sin(
sin(![]() -
-![]() ).
).
故由2kπ-![]() ≤
≤![]() -
-![]() ≤2kπ+
≤2kπ+![]()
![]() 3kπ-
3kπ-![]() ≤x≤3kπ+
≤x≤3kπ+![]() (k∈Z),为单调减区间;
(k∈Z),为单调减区间;
由2kπ+![]() ≤
≤![]() -
-![]() ≤2kπ+
≤2kπ+![]() 3kπ+
3kπ+![]() ≤x≤3kπ+
≤x≤3kπ+![]() (k∈Z),为单调增区间.
(k∈Z),为单调增区间.
∴递减区间为[3kπ-![]() ,3kπ+
,3kπ+![]() ],
],
递增区间为[3kπ+![]() ,3kπ+
,3kπ+![]() ] (k∈Z).
] (k∈Z).
(2)y=-|sin(x+![]() )|的图象的增区间为[kπ-
)|的图象的增区间为[kπ-![]() ,kπ+
,kπ+![]() ],减区间为[kπ+
],减区间为[kπ+![]() ,kπ+
,kπ+![]() ].
].
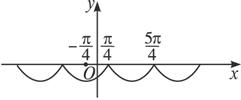
(2)不用图象能求解吗?
提示:y=-![]() =-
=-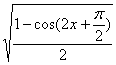 =-
=-![]() .
.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 ; (2)y=
; (2)y= tan2x+1;
tan2x+1;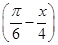 .
.