题目内容
求下列函数的单调区间:
(1)f(x)=
+sinx;
(2)f(x)=
.
(1)f(x)=
| x |
| 2 |
(2)f(x)=
| 2x-b |
| (x-1)2 |
分析:(1)求导数f′(x),然后解不等式f′(x)>0,f′(x)<0可得函数的增减区间;
(2)求导数f′(x),然后按照b的取值范围分类讨论解不等式f′(x)>0,f′(x)<0;
(2)求导数f′(x),然后按照b的取值范围分类讨论解不等式f′(x)>0,f′(x)<0;
解答:解:(1)f′(x)=
+cosx,
令f′(x)<0,即cosx<-
,解得
π+2kπ<x<
π+2kπ,k∈Z,
令f′(x)>0,即cosx>-
,解得-
π+2kπ<x<
π+2kπ,k∈Z,
所以函数f(x)的单调减区间为(
π+2kπ,
π+2kπ),k∈Z,单调增区间为(-
π+2kπ,
π+2kπ),k∈Z;
(2)f′(x)=
=
=-
,
令f′(x)=0,得x=b-1,
当b-1<1即b<2时,由f′(x)>0得b-1<x<1,由f′(x)<0得x<b-1或x>1,
当b-1>1即b>2时,由f′(x)>0得1<x<b-1,由f′(x)<0得x<1或x>b-1,
所以当b<2时,f(x)的减区间为(-∞,b-1)和(1,+∞),增区间为(b-1,1);
当b>2时,f(x)的减区间为(-∞,1)和(b-1,+∞),增区间为(1,b-1);
当b=2时,f(x)的减区间为(-∞,1)和(1,∞).
| 1 |
| 2 |
令f′(x)<0,即cosx<-
| 1 |
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
令f′(x)>0,即cosx>-
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
所以函数f(x)的单调减区间为(
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
(2)f′(x)=
| 2(x-1)2-(2x-b)•2(x-1) |
| (x-1)4 |
| -2x+2b-2 |
| (x-1)3 |
| 2[x-(b-1)] |
| (x-1)3 |
令f′(x)=0,得x=b-1,
当b-1<1即b<2时,由f′(x)>0得b-1<x<1,由f′(x)<0得x<b-1或x>1,
当b-1>1即b>2时,由f′(x)>0得1<x<b-1,由f′(x)<0得x<1或x>b-1,
所以当b<2时,f(x)的减区间为(-∞,b-1)和(1,+∞),增区间为(b-1,1);
当b>2时,f(x)的减区间为(-∞,1)和(b-1,+∞),增区间为(1,b-1);
当b=2时,f(x)的减区间为(-∞,1)和(1,∞).
点评:本题考查利用导数研究函数的单调性,考查分类讨论思想,属中档题.

练习册系列答案
相关题目
 ; (2)y=
; (2)y= tan2x+1;
tan2x+1;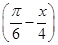 .
.