题目内容
求下列函数的单调区间:(1)y=
| 1 |
| 2 |
| π |
| 4 |
| 2x |
| 3 |
| π |
| 4 |
分析:(1)要将原函数化为y=-
sin(
x-
)再求之.
(2)可画出y=-|sin(x+
)|的图象.
| 1 |
| 2 |
| 2 |
| 3 |
| π |
| 4 |
(2)可画出y=-|sin(x+
| π |
| 4 |
解答: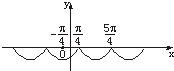 解:(1)y=
解:(1)y=
sin(
-
)=-
sin(
-
).
故由 2kπ-
≤
-
≤2kπ+
?3kπ-
≤x≤3kπ+
(k∈Z),为单调减区间;
由 2kπ+
≤
-
≤2kπ+
?3kπ+
≤x≤3kπ+
(k∈Z),为单调增区间.
∴递减区间为[3kπ-
,3kπ+
],
递增区间为[3kπ+
,3kπ+
](k∈Z).
(2)y=-|sin(x+
)|的图象的增区间为[kπ-
,kπ+
],
减区间为[kπ+
,kπ+
].
深化拓展:(2)不用图象能求解吗?
提示:y=-
=-
=-
 解:(1)y=
解:(1)y=| 1 |
| 2 |
| π |
| 4 |
| 2x |
| 3 |
| 1 |
| 2 |
| 2x |
| 3 |
| π |
| 4 |
故由 2kπ-
| π |
| 2 |
| 2x |
| 3 |
| π |
| 4 |
| π |
| 2 |
?3kπ-
| 3π |
| 8 |
| 9π |
| 8 |
由 2kπ+
| π |
| 2 |
| 2x |
| 3 |
| π |
| 4 |
| 3π |
| 2 |
?3kπ+
| 9π |
| 8 |
| 21π |
| 8 |
∴递减区间为[3kπ-
| 3π |
| 8 |
| 9π |
| 8 |
递增区间为[3kπ+
| 9π |
| 8 |
| 21π |
| 8 |
(2)y=-|sin(x+
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
减区间为[kπ+
| π |
| 4 |
| 3π |
| 4 |
深化拓展:(2)不用图象能求解吗?
提示:y=-
sin2(x+
|
|
|
点评:本题将三角函数与函数的单调性很好的结合,考查三角函数的单调区间.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 ; (2)y=
; (2)y= tan2x+1;
tan2x+1;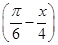 .
.