题目内容
已知函数 ,
, ,且函数
,且函数 在点
在点 处的切线方程为
处的切线方程为 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)设点 ,当
,当 时,直线
时,直线 的斜率恒小于
的斜率恒小于 ,试求实数
,试求实数 的取值范围;
的取值范围;
(Ⅲ)证明: .
.
(Ⅰ)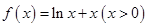 ;(Ⅱ)
;(Ⅱ)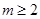 ;(Ⅲ)详见解析.
;(Ⅲ)详见解析.
解析试题分析:(Ⅰ)根据函数 在点
在点 处的切线方程为
处的切线方程为 ,这一条件分离出两个条件
,这一条件分离出两个条件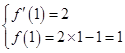 ,然后根据这两个条件列有关
,然后根据这两个条件列有关 和
和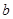 的二元一次方程组,解出
的二元一次方程组,解出 和
和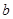 的值进而确定函数
的值进而确定函数 的解析式;(Ⅱ)先将直线
的解析式;(Ⅱ)先将直线 的斜率利用点
的斜率利用点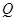 的坐标表示,然后建立以
的坐标表示,然后建立以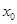 为自变量的函数,对参数
为自变量的函数,对参数 进行分类讨论,即可求出参数
进行分类讨论,即可求出参数 的取值范围;(Ⅲ)证明不等式
的取值范围;(Ⅲ)证明不等式 ,构造函数
,构造函数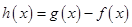 ,等价转化为
,等价转化为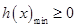 ,借助极小值,但同时需要注意有些时候相应整体的代换.
,借助极小值,但同时需要注意有些时候相应整体的代换.
试题解析:(Ⅰ)
 ,
,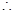
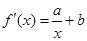 . 1分
. 1分 函数
函数 在点
在点 处的切线方程为
处的切线方程为 ,
,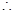
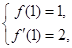 即
即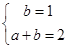 , 解得
, 解得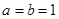 , 2分
, 2分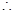
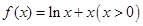 . 3分
. 3分
(Ⅱ)由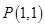 、
、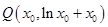 ,得
,得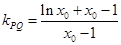 ,
,
∴“当 时,直线
时,直线 的斜率恒小于
的斜率恒小于 ”
” 当
当 时,
时,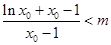 恒成立
恒成立
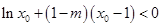 对
对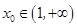 恒成立. 4分
恒成立. 4分
令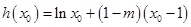 ,
,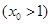 .
.
则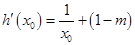
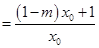 , 5分
, 5分
(ⅰ)当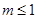 时,由
时,由 ,知
,知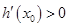 恒成立,
恒成立,
∴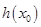 在
在 单调递增,
单调递增,
∴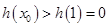 ,不满足题意的要求. 6分
,不满足题意的要求. 6分
(ⅱ)当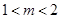 时,
时,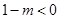 ,
,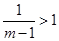 ,
,
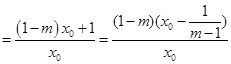 ,
,
∴当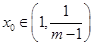 ,
,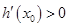 ;当
;当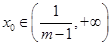 ,
,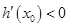 .
.
即
练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛 ,要求
,要求 在
在 的延长线上,
的延长线上, 在
在 的延长线上,且对角线
的延长线上,且对角线 过
过 点.已知
点.已知 米,
米, 米。
米。
 (单位:米),要使花坛
(单位:米),要使花坛 的取值范围;
的取值范围;  (单位:米),则当
(单位:米),则当 ,
, 的长度分别是多少时,花坛
的长度分别是多少时,花坛 .
. 的图象在
的图象在 处的切线斜率为
处的切线斜率为 ,求实数
,求实数 的值;
的值; 在
在 上是减函数,求实数
上是减函数,求实数 ,
, 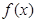 的极大值;
的极大值;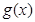 ,若
,若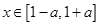 时,恒有
时,恒有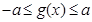 成立,试确定实数
成立,试确定实数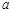 的取值范围.
的取值范围.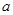 、
、 、
、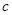 都是实数,函数
都是实数,函数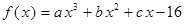 的导函数为
的导函数为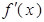 ,
,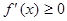 的解集为
的解集为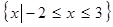 .
.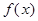 的极大值等于
的极大值等于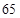 ,求
,求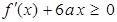 的解集为集合
的解集为集合 ,当
,当 时,函数
时,函数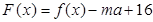 只有一个零点,求实数
只有一个零点,求实数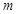 的取值范围.
的取值范围. ,求证:
,求证: .
. (
( 为常数),且
为常数),且 在点
在点 处的切线平行于
处的切线平行于 轴.
轴.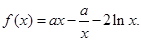
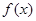 在
在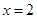 时有极值,求实数
时有极值,求实数 的值和
的值和
 取值范围.
取值范围.