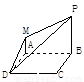题目内容
把矩形ABCD沿对角线BD折成二面角A-BD-C，若AB=2，
，
，则二面角A-BD-C的大小为（ ）A．150°
B．120°
C．60°
D．30°
【答案】分析：过A点做AE⊥BD于E，过C点做CF⊥BD于F，根据已知矩形ABCD中AB=2，
，分别求出AE，CF，EF的长，代入异面直线上两点间距离公式，构造关于θ的三角方程，即可求出二面角A-BD-C的大小．
解答：解：过A点做AE⊥BD于E，过C点做CF⊥BD于F
则AE=CF=
，EF=2
设二面角A-BD-C的大小为θ
则AC=
=
=
则cosθ=
则θ=60°
故选C
点评：本题考查的知识点是二面角的平面角及求法，其中根据二面角的定义，分别过A点做AE⊥BD于E，过C点做CF⊥BD于F，从而将二面角问题转化为异面直线的夹角问题，是解答本题的关键．
，分别求出AE，CF，EF的长，代入异面直线上两点间距离公式，构造关于θ的三角方程，即可求出二面角A-BD-C的大小．解答：解：过A点做AE⊥BD于E，过C点做CF⊥BD于F
则AE=CF=
，EF=2设二面角A-BD-C的大小为θ
则AC=
==则cosθ=
则θ=60°
故选C
点评：本题考查的知识点是二面角的平面角及求法，其中根据二面角的定义，分别过A点做AE⊥BD于E，过C点做CF⊥BD于F，从而将二面角问题转化为异面直线的夹角问题，是解答本题的关键．
练习册系列答案
相关题目
把矩形ABCD沿对角线BD折成二面角A-BD-C，若AB=2，AD=2
，AC=
，则二面角A-BD-C的大小为（ ）
| 3 |
| 7 |
| A、150° | B、120° |
| C、60° | D、30° |
，且
，求二面角A－BD－C的大小．
的矩形ABCD沿对角线AC折成直二面角B—AC—D且使A、B、C、D四点在同一球面上，则该球的体积为
▲
，E，F，G，H分别是VA，VB，BC，AC的