题目内容
某学校的生物实验室里有一个鱼缸,里面有6条鱼,其中4条黑色的和2条红色的,有位生物老师每周4天有课,每天上、下各一节课,每节课前从鱼缸中任取1条鱼在课上用,用后再放回鱼缸.
(1)求这位生物老师在一天中上、下午所捞的鱼为同色的概率;
(2)求这位生物老师一周中恰有两天上、下午所捞得的鱼为不同色的概率.
(1)求这位生物老师在一天中上、下午所捞的鱼为同色的概率;
(2)求这位生物老师一周中恰有两天上、下午所捞得的鱼为不同色的概率.
考点:相互独立事件的概率乘法公式,互斥事件的概率加法公式
专题:概率与统计
分析:(1)一天中上、下午所捞的鱼同为黑色鱼和同为红色鱼为互斥事件,结合相互独立事件概率乘法公式,和互斥事件概率加法公式,可得答案.
(2)恰有两天不同色的概率为
(
)2(
)2,计算可得答案.
(2)恰有两天不同色的概率为
| C | 2 4 |
| 5 |
| 9 |
| 4 |
| 9 |
解答:
解:(1)设一天中上、下午所捞的鱼同为黑色鱼的概率为p1,同为红色鱼的概率为p2,
则p=p1+p2=
•
+
•
=
.
答:这位生物老师在一天中上、下午所捞的鱼为同色的概率为
.
(2)恰有两天不同色的概率为P′=
(
)2(
)2=
=
.
答:这位生物老师一周中恰有两天上、下午所捞得的鱼为不同的概率
.
则p=p1+p2=
| 4 |
| 6 |
| 4 |
| 6 |
| 2 |
| 6 |
| 2 |
| 6 |
| 5 |
| 9 |
答:这位生物老师在一天中上、下午所捞的鱼为同色的概率为
| 5 |
| 9 |
(2)恰有两天不同色的概率为P′=
| C | 2 4 |
| 5 |
| 9 |
| 4 |
| 9 |
| 6×25×16 |
| 81×81 |
| 800 |
| 2187 |
答:这位生物老师一周中恰有两天上、下午所捞得的鱼为不同的概率
| 800 |
| 2187 |
点评:本意考查互斥事件、相互独立事件的概率计算,熟练掌握相互独立事件概率乘法公式,和互斥事件概率加法公式,是解答的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
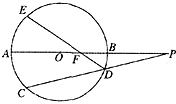 已知⊙O的半径R=2,P为直径AB延长线上一点,PB=3,割线PDC交⊙O于D,C两点,E为⊙O上一点,且
已知⊙O的半径R=2,P为直径AB延长线上一点,PB=3,割线PDC交⊙O于D,C两点,E为⊙O上一点,且