题目内容
已知双曲线 的左右焦点分别为
的左右焦点分别为 ,其一条渐近线方程为
,其一条渐近线方程为 ,点
,点 在该双曲线上,则
在该双曲线上,则 = ( )
= ( )
 的左右焦点分别为
的左右焦点分别为 ,其一条渐近线方程为
,其一条渐近线方程为 ,点
,点 在该双曲线上,则
在该双曲线上,则 = ( )
= ( )A. | B. | C.0 | D.4 |
C
分析:由题设知b=
 ,再根据点
,再根据点 在该双曲线上知y
在该双曲线上知y =1.由此能求出
=1.由此能求出  ?
?  .
.解答:解:∵双曲线
 的渐近线方程为y=±
的渐近线方程为y=± bx=±x,
bx=±x,∴b=
 .
.把点
 代入双曲线,得
代入双曲线,得 -
- =1,解得y
=1,解得y =1.
=1.∴P(
 ,1),F
,1),F (-2,0),F
(-2,0),F (2,0),
(2,0), ?
?  .=(-2-
.=(-2- ,0-1)?(2-
,0-1)?(2- ,0-1)=0,
,0-1)=0,或P(
 ,-1),F
,-1),F (-2,0),F
(-2,0),F (2,0),
(2,0), ?
?  =(-2-
=(-2- ,0+1)?(2-
,0+1)?(2- ,0+1)=0.
,0+1)=0.故答案为0.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 的离心率为2,焦点与椭圆
的离心率为2,焦点与椭圆 的焦点相同,求双曲
的焦点相同,求双曲 线的方程及焦点坐标
线的方程及焦点坐标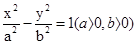 的离心率为
的离心率为 ,且它的一条准线与抛物线y2=4x的准线重合,则此抛物线的方程为( )
,且它的一条准线与抛物线y2=4x的准线重合,则此抛物线的方程为( )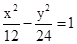
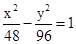
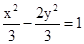
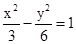
 的根
的根 是双曲线S的一条渐近线,而且原点O,点A(a,0)和点B(0,-b)使等式
是双曲线S的一条渐近线,而且原点O,点A(a,0)和点B(0,-b)使等式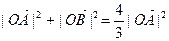 ·
· 成立.
成立.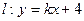 对称,求实数k的取值范围.
对称,求实数k的取值范围. 的一条准线与抛物线
的一条准线与抛物线 的准线重合,则该双曲线的离心率为 ( )
的准线重合,则该双曲线的离心率为 ( ) 



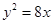 上一点
上一点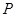 到其焦点的距离为
到其焦点的距离为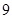 ,则点
,则点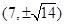



 中,已知双曲线
中,已知双曲线 的焦点到一条渐近线
的焦点到一条渐近线 的距离为4,若渐近线
的距离为4,若渐近线 在原点处的切线,则双曲线的标准方程为 ▲ .
在原点处的切线,则双曲线的标准方程为 ▲ .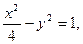
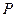 为C上的任意点.
为C上的任意点.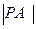 的最小值.
的最小值.