题目内容
10.“a=2”是“函数f(x)=xa-2为偶函数”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 利用充分条件和必要条件的定义,结合偶函数的定义进行判断.
解答 解;当a=2,f(x)=xa-2=x2-2,
则f(-x)=(-x)2-2=x2-2=f(x),所以f(x)是偶函数.
当a=4时,函数f(x)=x4-2为偶函数,但a=2不成立.
所以“a=2”是“函数f(x)=xα-2为偶函数”的充分不必要条件.
故选A.
点评 本题主要考查充分条件和必要条件的判断,要熟练掌握函数奇偶性的定义,比较基础.

练习册系列答案
相关题目
19.2007年10月27日全国人大通过了关于修改个所得税的决定,工薪所得减去费用标准从800元提高到1600元,也就是说原来月收入超过800元部分就要纳税,2008年1月1日开始超过1600元才纳税,若税法修改前后超过部分的税率相同,如表:
某人2007年6月交纳个人所得税123元,则按照新税法只要交43元.
| 级数 | 全月应纳税所得额 | 税率(%) |
| 1 | 不超过500元 | 5 |
| 2 | 500~2000元 | 10 |
| 3 | 2000~5000元 | 15 |
5.已知关于x的不等式ax2+2x+b>0(a≠0)的解集是{x|x≠-$\frac{1}{a}$,x∈R},且a>b,则$\frac{{a}^{2}+{b}^{2}}{a-b}$的最小值是( )
| A. | 2$\sqrt{2}$ | B. | 2 | C. | $\sqrt{2}$ | D. | 1 |
2.设集合S={y|y=2x,x∈R},T={(x,y)|y=x2+1,x∈R},则S∩T是( )
| A. | ∅ | B. | {0} | C. | {(0,1)}和{(1,2)} | D. | {1} |
18.函数y=2sin(-x+$\frac{π}{6}$)在下列哪个区间上增函数( )
| A. | [$\frac{5π}{6}$,$\frac{11π}{6}$] | B. | [$\frac{2π}{3}$,$\frac{5π}{3}$] | C. | [$\frac{π}{2}$,$\frac{3π}{2}$] | D. | [-$\frac{π}{2}$,0] |
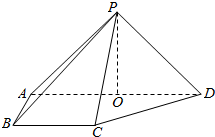 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.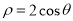 ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是
,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是 (t为参数).
(t为参数).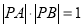 ,求实数m的值.
,求实数m的值.