题目内容
如图，在几何体ABC－A1B1C1中，点A1，B1，C1在平面ABC内的正投影分别为A，B，C，且AB⊥BC，E为AB1中点，AB＝AA1＝BB1＝2CC1.求证
(1)CE∥平面A1B1C1；
(2)平面AB1C1⊥平面A1BC.
证明：(1)由题知AA1⊥平面ABC，BB1⊥平面ABC，CC1⊥平面ABC，
∴AA1∥BB1∥CC1.
如图，取A1B1中点F，连接EF，FC1.
∵E为AB1中点，∴EF綊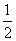
A1A，
又AA1＝2CC1，∴CC1綊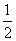AA1，
∴EE綊CC1，∴四边形EFC1C为平行四边形，
∴CE∥C1F，
又CE⊄平面A1B1C1，C1F⊂平面A1B1C1，
∴CE∥平面A1B1C1.
(2)∵BB1⊥平面ABC，∴BB1⊥BC，
又AB⊥BC，AB∩BB1＝B，
∴BC⊥平面AA1B1B，
∵AB1⊂平面AA1B1B，∴BC⊥AB1，
∵AA1＝BB1＝AB，AA1∥BB1，
∴四边形AA1B1B为正方形，∴AB1⊥A1B，
∵A1B∩BC＝B，
∴AB1⊥平面A1BC，
∵AB1⊂平面AB1C1，
∴平面AB1C1⊥平面A1BC
练习册系列答案
相关题目
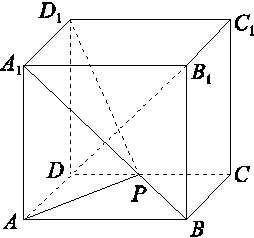
的正三角形，侧棱垂直于底面，且该三棱柱的外接球的表面积为12π，则该三棱柱的体积为________．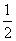
x＋a，则函数f(x)的零点个数是( )
的最小值是( )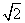
C．4 D．4