题目内容
5、偶函数f （x） 在区间[0，+∞）的图象如右，则函数f （x）的单调增区间为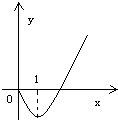
[-1，0]，[1，+∞）
．分析：由图象得出f （x） 在区间[0，+∞）的单调区间，再由偶函数的对称性得出（-∞，0）上的函数的单调区间即可得出答案
解答：解：由图知函数在[0，1]减，在[1，+∞）上增
由偶函数的对称性知（-∞，0）上函数的增区间为[-1，0]
函数f （x）的单调增区间为[-1，0]，[1，+∞）
故答案为[-1，0]，[1，+∞）
由偶函数的对称性知（-∞，0）上函数的增区间为[-1，0]
函数f （x）的单调增区间为[-1，0]，[1，+∞）
故答案为[-1，0]，[1，+∞）
点评：本题考查偶函数，解题的关键是正确识图以及掌握偶函数的对称性，其规律是在对称的区间上函数的单调性相反．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知偶函数f（x）在区间[0，+∞）单调递增，则满足f（
）＜f（x）的x取值范围是（ ）
| x+2 |
| A、（2，+∞） |
| B、（-∞，-1）∪（2，+∞） |
| C、[-2，-1）∪（2，+∞） |
| D、（-1，2） |
已知定义域为R的偶函数f（x）在（-∞，0]上是减函数，且f(
)=0，则不等式f（log2x）＞0的解集为（ ）
| 1 |
| 2 |
A、(0，
| ||||||
B、(
| ||||||
C、(0，
| ||||||
D、(0，
|