题目内容
在抛物线y2=-4x上求一点P,使其到焦点F的距离与到A(-2,1)的距离之和最小,则该点的坐标是 .
分析:根据抛物线方程求得抛物线的焦点为F(-1,0)、准线为x=1.设点P在准线上的射影为Q,根据抛物线的定义得|PQ|+|PA|=|PF|+|PA|,利用平面几何知识得当A、P、Q三点共线时,这个距离之和达到最小值,此时P点的纵坐标为1,利用抛物线方程求出P的横坐标,从而可得答案.
解答:解:由抛物线方程为y2=-4x,可得2p=4,
=1,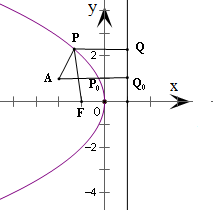
∴焦点坐标为F(-1,0),准线方程为x=1.
设点P在准线上的射影为Q,连结PQ,
则根据抛物线的定义得|PF|=|PQ|,
由平面几何知识,可知当A、P、Q三点共线时,
|PQ|+|PA|达到最小值,此时|PF|+|PA|也达到最小值.
∴|PF|+|PA|最小蝗,点P的纵坐标为1,
将P(x,1)代入抛物线方程,得12=-4x,解得x=-
,
∴使P到A、F距离之和最小的点P坐标为(-
,1).
故答案为:(-
,1)
| p |
| 2 |

∴焦点坐标为F(-1,0),准线方程为x=1.
设点P在准线上的射影为Q,连结PQ,
则根据抛物线的定义得|PF|=|PQ|,
由平面几何知识,可知当A、P、Q三点共线时,
|PQ|+|PA|达到最小值,此时|PF|+|PA|也达到最小值.
∴|PF|+|PA|最小蝗,点P的纵坐标为1,
将P(x,1)代入抛物线方程,得12=-4x,解得x=-
| 1 |
| 4 |
∴使P到A、F距离之和最小的点P坐标为(-
| 1 |
| 4 |
故答案为:(-
| 1 |
| 4 |
点评:本题主要考查了抛物线的定义,充分利用了抛物线上的点到准线的距离与点到焦点的距离相等这一特性,运用了转化思想和数形结合思,本题属于基础题.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目