题目内容
如图1,A(-1,0)、B(1,0)是椭圆
+
=1(a>b>0)的长轴上两点,C,D分别为椭圆的短轴和长轴的端点,P是CD上的动点,若
•
的最大值与最小值分别为3、
.
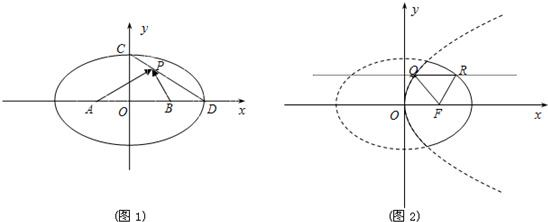
(1)求椭圆的离心率;
(2)如图2,点F(1,0),动点Q、R分别在抛物线y2=4x及椭圆
+
=1(a>b>0)的实线部分上运动,且QR∥x轴,求△FQR的周长l的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| AP |
| BP |
| 5 |
| 7 |

(1)求椭圆的离心率;
(2)如图2,点F(1,0),动点Q、R分别在抛物线y2=4x及椭圆
| x2 |
| a2 |
| y2 |
| b2 |
分析:(1)设P(x1,y1),则
=(x1+1,y1),
=(x1-1,y1),故
•
=x12+y12-1,由此能求出椭圆的离心率.
(2)设R(x0,y0),由抛物线的定义知QF等于点Q到抛物线准线x=1的距离,故QF+QR等于点R到抛物线准线x=1的距离为x0+1.由椭圆的第二定义知QF=
(4-x0),由此能求出△FQR的周长l的取值范围.
| AP |
| BP |
| AP |
| BP |
(2)设R(x0,y0),由抛物线的定义知QF等于点Q到抛物线准线x=1的距离,故QF+QR等于点R到抛物线准线x=1的距离为x0+1.由椭圆的第二定义知QF=
| 1 |
| 2 |
解答:解:(1)设P(x1,y1),则
=(x1+1,y1),
=(x1-1,y1),
∴
•
=x12+y12-1,…(2分)
∵
•
的最大值与最小值分别为3和
,
∴x12+y12的最大值与最小值分别为4、
,…(3分)
而x12+y12表示线段CD上的点到原点的距离OP的平方,
∴点OP的最大值为OD=2,
即a=2,…(5分)
OP的最小值即为O到线段CD的距离
,
由平面几何知识得OC=
,即b=
,…(7分)
得c=
=1,则椭圆的离心率e=
=
.…(9分)
(2)设R(x0,y0),
由抛物线的定义知QF等于点Q到抛物线准线x=1的距离,
∴QF+QR等于点R到抛物线准线x=1的距离为x0+1,…(11分)
由椭圆的第二定义知QF=
(4-x0),
∴△NAB的周长l=x0+1+
(4-x0)=3+
x0.…(13分)
由
,
得:抛物线与椭圆交点的横坐标为
,
即得
<x0<2.
所以△FQR的周长l的取值范围为(
,4).…(16分)
| AP |
| BP |
∴
| AP |
| BP |
∵
| AP |
| BP |
| 5 |
| 7 |
∴x12+y12的最大值与最小值分别为4、
| 12 |
| 7 |
而x12+y12表示线段CD上的点到原点的距离OP的平方,
∴点OP的最大值为OD=2,
即a=2,…(5分)
OP的最小值即为O到线段CD的距离
2
| ||
| 7 |
由平面几何知识得OC=
| 3 |
| 3 |
得c=
| a2-b2 |
| c |
| a |
| 1 |
| 2 |
(2)设R(x0,y0),
由抛物线的定义知QF等于点Q到抛物线准线x=1的距离,
∴QF+QR等于点R到抛物线准线x=1的距离为x0+1,…(11分)
由椭圆的第二定义知QF=
| 1 |
| 2 |
∴△NAB的周长l=x0+1+
| 1 |
| 2 |
| 1 |
| 2 |
由
|
得:抛物线与椭圆交点的横坐标为
| 2 |
| 3 |
即得
| 2 |
| 3 |
所以△FQR的周长l的取值范围为(
| 10 |
| 3 |
点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,抛物线的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
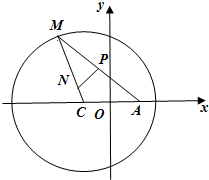 已知圆C:(x+1)2+y2=8.
已知圆C:(x+1)2+y2=8.
 的长轴上两点,C,D分别为椭圆的短轴和长轴的端点,P是CD上的动点,若
的长轴上两点,C,D分别为椭圆的短轴和长轴的端点,P是CD上的动点,若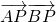 的最大值与最小值分别为3、
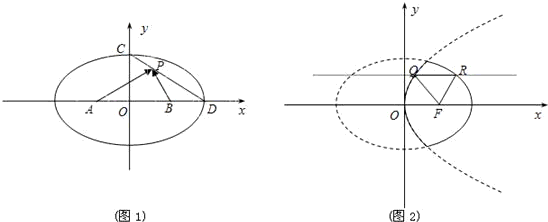
的最大值与最小值分别为3、 .
.
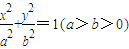 的长轴上两点,C,D分别为椭圆的短轴和长轴的端点,P是CD上的动点,若
的长轴上两点,C,D分别为椭圆的短轴和长轴的端点,P是CD上的动点,若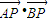 的最大值与最小值分别为3、
的最大值与最小值分别为3、 .
.
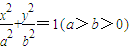 的实线部分上运动,且QR∥x轴,求△FQR的周长l的取值范围.
的实线部分上运动,且QR∥x轴,求△FQR的周长l的取值范围.