题目内容
已知函数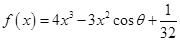 ,其中
,其中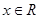 ,
,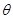 为参数,且
为参数,且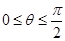 .
.
(1)当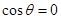 时,判断函数
时,判断函数 是否有极值;
是否有极值;
(2)要使函数 的极小值大于零,求参数
的极小值大于零,求参数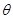 的取值范围;
的取值范围;
(3)若对(2)中所求的取值范围内的任意参数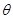 ,函数
,函数 在区间
在区间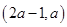 内都是增函数,求实数
内都是增函数,求实数 的取值范围.
的取值范围.
(1) 无极值;(2)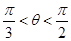 ;(3)
;(3) .
.
解析试题分析:(1) 当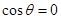 时,
时, ,利用函数单调性的定义或导数法可证明
,利用函数单调性的定义或导数法可证明 在
在 内是增函数,故无极值;(2)先求函数
内是增函数,故无极值;(2)先求函数 的导数:
的导数: ,令
,令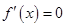 ,得可能的极值点:
,得可能的极值点: .由
.由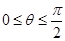 及(1),只需考虑
及(1),只需考虑 的情况,列表考虑当
的情况,列表考虑当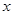 变化时,
变化时, 的符号及
的符号及 的变化情况,求得函数
的变化情况,求得函数 的极小值,最后根据题意列极小值大于零的不等式,解不等式求出参数
的极小值,最后根据题意列极小值大于零的不等式,解不等式求出参数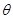 的取值范围;(3)由(2)知,函数
的取值范围;(3)由(2)知,函数 在区间
在区间 与
与 内都是增函数.由题设,函数
内都是增函数.由题设,函数 在
在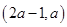 内是增函数,因而
内是增函数,因而 必须满足不等式组
必须满足不等式组 或
或 进而可求得
进而可求得 的取值范围.
的取值范围.
试题解析:(1)当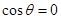 时,
时, ,则
,则 在
在 内是增函数,故无极值.
内是增函数,故无极值.
(2) ,令
,令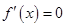 ,得
,得 .由
.由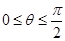 及(1),只需考虑
及(1),只需考虑 的情况.当
的情况.当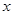 变化时,
变化时, 的符号及
的符号及 的变化情况如下表:
的变化情况如下表: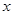

0 



+ 0 - 0 + 
↗  练习册系列答案
练习册系列答案
培优竞赛超级课堂系列答案
黄冈小状元达标卷系列答案

高效精练系列答案
练与测联动课堂系列答案
赢在新课堂系列答案
通城学典非常课课通系列答案
高分拔尖提优训练系列答案
聚焦课堂高效学习直通车系列答案
小题巧练系列答案
相关题目
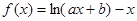 ,其中
,其中 ,
, ,
,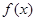 为
为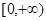 上的减函数,求
上的减函数,求 应满足的关系;
应满足的关系;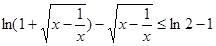 。
。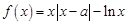 ,
,
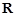 .
.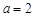 ,求函数
,求函数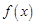 在区间
在区间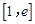 上的最值;
上的最值;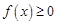 恒成立,求
恒成立,求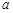 的取值范围. 注:
的取值范围. 注: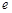 是自然对数的底数.
是自然对数的底数.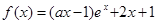 在
在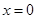 处取得极值.
处取得极值. 的值;
的值; 时,
时, .
.
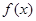 在点
在点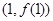 处的切线与圆
处的切线与圆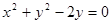 相切,求
相切,求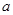 的值;
的值; 时,函数
时,函数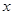 轴的上方,试求出
轴的上方,试求出 .
.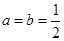 时,求函数
时,求函数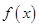 的最大值;
的最大值;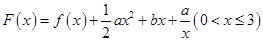 其图象上任意一点
其图象上任意一点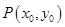 处切线的斜率
处切线的斜率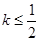 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;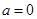 ,
, ,方程
,方程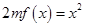 有唯一实数解,求正数
有唯一实数解,求正数 的值.
的值.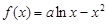 .
. 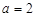 时,求函数
时,求函数 在
在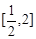 上的最大值;
上的最大值;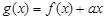 ,若
,若 在区间
在区间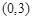 上不单调,求
上不单调,求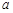 的取值范围;
的取值范围;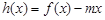 的图象与
的图象与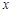 轴交于两点
轴交于两点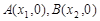 ,且
,且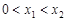 ,又
,又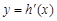 是
是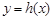 的导函数.若正常数
的导函数.若正常数 满足条件
满足条件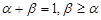 ,证明:
,证明: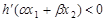 .
.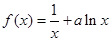 (
( ≠0,
≠0,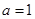 ,求函数
,求函数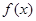 的极值和单调区间;
的极值和单调区间;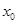 ,使得
,使得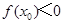 成立,求实数
成立,求实数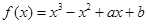 .
. 在
在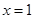 处取得极值,且函数
处取得极值,且函数 的取值范围.
的取值范围. 上不是单调函数,求
上不是单调函数,求 的取值范围.
的取值范围.