题目内容
已知函数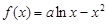 .
.
(1)当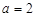 时,求函数
时,求函数 在
在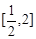 上的最大值;
上的最大值;
(2)令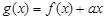 ,若
,若 在区间
在区间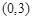 上不单调,求
上不单调,求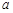 的取值范围;
的取值范围;
(3)当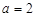 时,函数
时,函数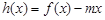 的图象与
的图象与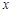 轴交于两点
轴交于两点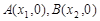 ,且
,且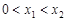 ,又
,又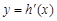 是
是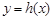 的导函数.若正常数
的导函数.若正常数 满足条件
满足条件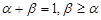 ,证明:
,证明: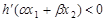 .
.
(1)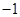 ;(2)
;(2)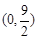 ;(3)详见解析.
;(3)详见解析.
解析试题分析:(1)当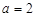 时,
时,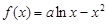 ,求其在
,求其在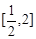 上的最大值,先要求出其导函数,然后利用导数的符号,判断函数的单调区间,最后就可求出函数的最大值;(2)函数在区间
上的最大值,先要求出其导函数,然后利用导数的符号,判断函数的单调区间,最后就可求出函数的最大值;(2)函数在区间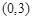 上不单调,而函数在在区间
上不单调,而函数在在区间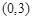 又是不间断的,则
又是不间断的,则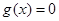 区间
区间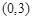 上有根且无重根,问题就转化为方程有解的问题,分离参数后又转化为函数的值域问题,这是我们所熟悉的问题;(3)根据
上有根且无重根,问题就转化为方程有解的问题,分离参数后又转化为函数的值域问题,这是我们所熟悉的问题;(3)根据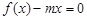 有两个实根
有两个实根 ,可得关于
,可得关于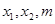 的两个等式,从而消去
的两个等式,从而消去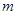 ,再将
,再将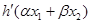 适当放缩后构造函数,通过判断函数的单调性去求函数的最值从而证明不等式.
适当放缩后构造函数,通过判断函数的单调性去求函数的最值从而证明不等式.
试题解析:(1) 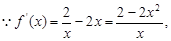 2分
2分
函数 在[
在[ ,1]是增函数,在[1,2]是减函数,
,1]是增函数,在[1,2]是减函数,
所以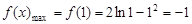 . 4分
. 4分
(2)因为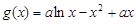 ,所以
,所以 , 5分
, 5分
因为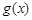 在区间
在区间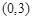 上不单调,所以
上不单调,所以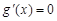 在(0,3)上有实数解,且无重根,
在(0,3)上有实数解,且无重根,
由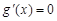 ,有
,有 =
= ,(
,( ) 6分
) 6分
又当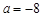 时,
时,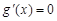 有重根
有重根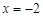 , 7分
, 7分
综上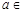
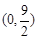 8分
8分
(3)∵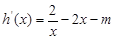 ,又
,又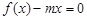 有两个实根
有两个实根 ,
,
∴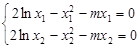 ,两式相减,得
,两式相减,得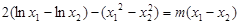 ,
,
∴ , 10分
, 10分
于是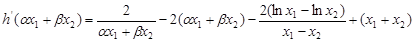
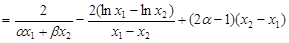 . 11分
. 11分 .
.
要证: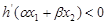 ,只需证:
,只需证: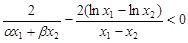
只需证: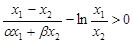 .(*) 12分
.(*) 12分
令 ,∴(*)化为
,∴(*)化为  ,只证
,只证
 ,其中
,其中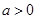 .
. ,求曲线
,求曲线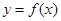 在点
在点 处的切线方程;
处的切线方程; 有三个零点,求
有三个零点,求 的取值范围.
的取值范围.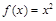 ,
,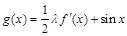 在
在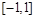 上的减函数.
上的减函数.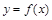 在点(1,f(1))处的切线方程;
在点(1,f(1))处的切线方程;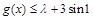 在
在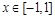 上恒成立,求
上恒成立,求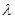 的取值范围;
的取值范围; 的方程
的方程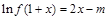 (
(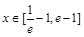 )有两个根(无理数e=2.71828),求m的取值范围.
)有两个根(无理数e=2.71828),求m的取值范围.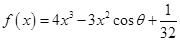 ,其中
,其中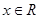 ,
,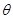 为参数,且
为参数,且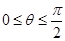 .
.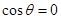 时,判断函数
时,判断函数 是否有极值;
是否有极值;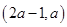 内都是增函数,求实数
内都是增函数,求实数 的取值范围.
的取值范围.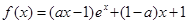 .
. 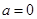 ,
,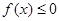 ;
;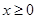 时,
时,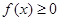 ,求
,求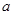 的取值范围.
的取值范围. 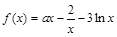 ,其中
,其中 为常数.
为常数.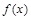 的图象在点
的图象在点 处的切线的斜率为1时,求函数
处的切线的斜率为1时,求函数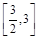 上的最小值;
上的最小值;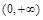 上既有极大值又有极小值,求实数
上既有极大值又有极小值,求实数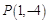 作函数
作函数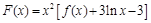 图象的切线,试问这样的切线有几条?并求这些切线的方程.
图象的切线,试问这样的切线有几条?并求这些切线的方程.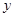 (单位:千套)与销售价格
(单位:千套)与销售价格 (单位:元/套)满足的关系式
(单位:元/套)满足的关系式 ,其中
,其中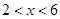 ,
, 为常数.已知销售价格为4元/套时,每日可售出套题21千套.
为常数.已知销售价格为4元/套时,每日可售出套题21千套. .
. 时,试确定函数
时,试确定函数 在其定义域内的单调性;
在其定义域内的单调性; 上的最小值;
上的最小值; .
. .
. 的单调区间;
的单调区间; ,
,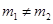 ,当
,当 时,有
时,有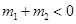 成立;
成立;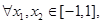
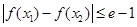 恒成立.求实数
恒成立.求实数 的取值范围.
的取值范围.