Question

 某人上楼梯，每步上一阶的概率为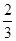，每步上二阶的概率为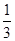，设该人从台阶下的平台开始出发，到达第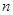阶的概率为.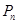

(1)求；;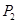

(2)该人共走了5步，求该人这5步共上的阶数ξ的数学期望.

 

Answer 1

【答案】

(1) P₂=×+；

(2)ξ的分布列为：

ξ	5	6	7	8	9	10
P

=5×()⁵+6×。

【解析】

试题分析：(1) 从平台到达第二阶有二种走法：走两步，或一步到达， 2分

故概率为P₂=×+         6分

(2)该人走了五步，共上的阶数ξ取值为5，6，7，8，9，10 .8分

ξ的分布列为：

ξ	5	6	7	8	9	10
P

         10分

=5×()⁵+6×    12分

考点：本题主要考查离散型随机变量的分布列和期望。

点评：中档题，这种类型是近几年高考题中经常出现的，考查离散型随机变量的分布列和期望，大型考试中理科考试必出的一道问题．的计算能力要求较高。