题目内容

某人上楼梯，每步上一阶的概率为
2
3
，每步上二阶的概率为
1
3
，设该人从台阶下的平台开始出发，到达第n阶的概率为Pn．
（Ⅰ）求P2；
（Ⅱ）该人共走了5步，求该人这5步共上的阶数ξ的数学期望．
分析：（1）由题意得：从平台到达第二阶有二种走法：走两步，或一步到达，由互斥事件的概率公式计算可得答案．
（2）该人走了五步，共上的阶数ξ取值为5，6，7，8，9，10．由题意得出ξ的分布列，进而根据公式求出其数学期望．
解答：解：（1）从平台到达第二阶有二种走法：走两步，或一步到达，
故概率为P2=
2
3
×
2
3
+
1
3
=
7
9

（2）该人走了五步，共上的阶数ξ取值为5，6，7，8，9，10   
ξ的分布列为：
ξ 5 6 7 8 9 10

P
C
0
5
(
2
3
)5
C
1
5
1
3
(
2
3
)4
C
2
5
( 
1
3
)2(
2
3
)3
C
3
5
(
1
3
)3(
2
3
)2
C
4
5
(
1
3
)4(
2
3
) 
C
5
5
(
1
3
)5
E（ξ）=5×（
2
3
）5+6×
C
1
5
1
3
(
2
3
)4+7×
C
2
5
(
1
3
)2(
2
3
)3+8×
C
3
5
(
1
3
)3(
2
3
)2+9×
C
4
5
(
1
3
)4(
2
3
) +10×
C
5
5
(
1
3
)5=
20
3
．
故该人这5步共上的阶数ξ的数学期望为
20
3
．
点评：解决此类问题的关键是准确把握条件，熟练掌握各种概率的计算公式．
练习册系列答案
相关题目

某人上楼梯,每步上一阶的概率为,每步上二阶的概率,设该人从台阶下的平台开始出发,到达第n阶的概率为Pn.

求P2;

该人共走了5,求该人这5步共上的阶数x的数学期望.

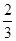 某人上楼梯，每步上一阶的概率为，每步上二阶的概率为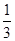，设该人从台阶下的平台开始出发，到达第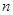阶的概率为.

(1)求；;

(2)该人共走了5步，求该人这5步共上的阶数ξ的数学期望.

 
某人上楼梯，每步上一阶的概率为
2
3
，每步上二阶的概率为
1
3
，设该人从台阶下的平台开始出发，到达第n阶的概率为Pn．
（Ⅰ）求P2；
（Ⅱ）该人共走了5步，求该人这5步共上的阶数ξ的数学期望．
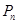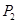某人上楼梯，每步上一阶的概率为，每步上二阶的概率为，设该人从台阶下的平台开始出发，到达第n阶的概率为Pn．
（Ⅰ）求P2；
（Ⅱ）该人共走了5步，求该人这5步共上的阶数ξ的数学期望．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网