题目内容
【题目】已知关于x的方程x2+2mx+2m+1=0(m∈R).
(1)若方程有两实根,其中一根在区间(﹣1,1)内,另一根在区间(1,2)内,求m的取值范围;
(2)若方程两实根均在区间(﹣1,2)内,求m的取值范围.
【答案】
(1)解:设f(x)=x2+2mx+2m+1,由题意可知:抛物线f(x)=x2+2mx+2m+1与x轴的交点分别
在区间(﹣1,1)和(1,2)内,
则  ,
,
解得﹣ ![]() <m<﹣
<m<﹣ ![]() ,
,
∴m 的取值范围为(﹣ ![]() ,﹣
,﹣ ![]() )
)
(2)解:若抛物线与x轴交点均落在区间(﹣1,2)内,则有 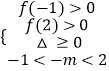 ,
,
即 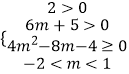 ,
,
解得:﹣ ![]() <m≤1﹣
<m≤1﹣ ![]()
∴m 的取值范围为(﹣ ![]() ,1﹣
,1﹣ ![]() ]
]
【解析】将方程根的问题转化为抛物线与x轴交点的问题进行解答,即可得到相的不等式组,解不等式组即可求得相应的m的取值范围.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

练习册系列答案
相关题目