题目内容
【题目】已知数列{an}的前n项和为Sn ， 对任意的n∈N* ， 点（n，Sn）恒在函数y= 
x的图象上．
（1）求数列{an}的通项公式；
（2）记Tn= 
，若对于一切的正整数n，总有Tn≤m成立，求实数m的取值范围；
（3）设Kn为数列{bn}的前n项和，其中bn=2an ， 问是否存在正整数n，t，使 
成立？若存在，求出正整数n，t；若不存在，请说明理由．
【答案】
（1）
解：由已知，得 
当n≥2时，an=Sn﹣Sn﹣1= 
=3n
当n=1时，a1=S1=3．∴an=3n
（2）
解： 
．
当n=1时，Tn+1＞Tn，即T2＞T1；当n=2时，Tn+1=Tn，即T3=T2；
当n≥3时，Tn+1＜Tn，即Tn＜Tn﹣1＜…＜T4＜T3
∴{Tn}中的最大值为 
，
要使Tn≤m对于一切的正整数n恒成立，只需 
∴ 
解法二： 
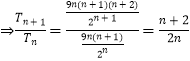
当n=1，2时，Tn+1≥Tn；当n≥3时，n+2＜2nTn+1＜Tn
∴n=1时，T1=9；n=2，3时， n≥4时，Tn＜T3
∴{Tn}中的最大值为 ，
要使Tn≤m对于一切的正整数n恒成立，只需 ∴
（3）
解： 
将Kn代入 
，化简得，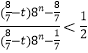 
（﹡）
若t=1时，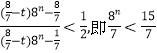 
，显然n=1时成立；
若t＞1时， 
（﹡）式化简为 
不可能成立
综上，存在正整数n=1，t=1使 成立
【解析】（1）利用an=Sn﹣Sn﹣1求解；（2）要使Tn≤m对于一切的正整数n恒成立，只需m≥{Tn}中的最大值即可；（3）求解有关正整数n的不等式．
练习册系列答案
优加精卷系列答案
相关题目
