题目内容
是否存在常数a, b使等式 对于一切n∈N*都成立?若存在,求出a, b的值,若不存在,请说明理由。
对于一切n∈N*都成立?若存在,求出a, b的值,若不存在,请说明理由。
解:若存在常数a,b使得等式成立,将n=1,n=2代入等式
有:


即有:
对于n为所有正整数是否成立,再用数学归纳法证明
证明:(1)当n=1时,等式成立。
(2)假设n=k时等式成立,即

当n=k+1时,即

也就是说n=k+1时,等式成立,
由(1)(2)可知等式对于任意的n∈N*都成立。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
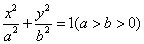 的离心率
的离心率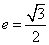 ,A,B是椭圆的左、右顶点,P是椭圆上不同于A,B的一点,直线PA,PB倾斜角分别为
,A,B是椭圆的左、右顶点,P是椭圆上不同于A,B的一点,直线PA,PB倾斜角分别为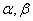 ,则
,则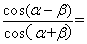
 的单调减区间为___________.
的单调减区间为___________.
 的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界),若点(1, 2)在“上”区域内,则双曲线离心率的取值范围为 。
的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界),若点(1, 2)在“上”区域内,则双曲线离心率的取值范围为 。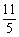 D.
D.
 C.98 D.49
C.98 D.49