题目内容
已知椭圆C：
＝1和点P(1,2)，直线l经过点P并与椭圆C交于A、B两点，求当l的倾斜角变化时，弦中点的轨迹方程．
解：设弦中点为M(x，y)，交点为A(x1，y1)，B(x2，y2)．当M与P不重合时，A、B、M、P四点共线．
∴(y2－y1)(x－1)＝(x2－x1)(y－2)，①
由
＋
＝1，
＋
＝1两式相减得
＝0.
又x1＋x2＝2x，y1＋y2＝2y，
由①②可得：9x2＋16y2－9x－32y＝0，③
当点M与点P重合时，点M坐标为(1,2)适合方程③，
∴弦中点的轨迹方程为：9x2＋16y2－9x－32y＝0.
练习册系列答案
相关题目
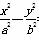＝1(a>0，b>0)的左顶点，F1、F2分别为双曲线的左、右焦点，P为双曲线上一点，G是△PF1F2的重心，若
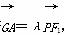，则双曲线的离心率为( )
，|AF|<|BF|，则|AF|＝________.