题目内容
已知数列{an}的前n项和为Sn,且Sn=2n2+n,n∈N*,数列{bn}满足an=4log2bn+3,n∈N*.
(1)求an,bn;
(2)求数列{an·bn}的前n项和Tn.
解:(1)由Sn=2n2+n,得
当n=1时,a1=S1=3;
当n≥2时,an=Sn-Sn-1=4n-1
所以an=4n-1,n∈N*
由4n-1=an=4 log2bn+3,得bn=2n-1,n∈N*.
(2)由(1)知anbn=(4n-1)·2n-1,n∈N*,
所以Tn=3+7×2+11×22+…+(4n-1)·2n-1,
2Tn=3×2+7×22+…+(4n-5)·2n-1+(4n-1)·2n,
所以2Tn-Tn=(4n-1)2n-[3+4(2+22+…+2n-1)]=(4n-5)2n+5
故Tn=(4n-5)2n+5,n∈N*.
练习册系列答案
相关题目
＝1和点P(1,2)，直线l经过点P并与椭圆C交于A、B两点，求当l的倾斜角变化时，弦中点的轨迹方程．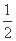
,a3=
,ak=
,则k等于( )
n}中的最大项是第k项,则k= . 
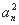-(2n-1)an-2n=0.
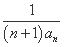,求数列{bn}的前n项和Tn.
-
+
+…+
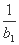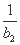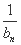,求T2012;
的图象是( )
